01. 푸리에 변환이란 https://infograph.tistory.com/220
01. 푸리에 변환이란
통신 이론, 디지털 신호, 음성처리 , 영상처리 등에서 항상 나오는 이론이 푸리에 변환이고, 가장 어려워하는 것이고, 내용을 이해하려고 많은 노력을 기울이면서도 정작 잘 파악이 안 되고, 다
infograph.tistory.com
02. 푸리에 급수 : 주기신호, 삼각 함수(사인, 코사인 그래프) https://infograph.tistory.com/221
02. 푸리에 급수 : 주기신호, 삼각 함수(사인, 코사인 그래프)
푸리에 변환을 바로 설명하기 전에 푸리에 급수부터 파악해볼 것이다. 푸리에 변환은 주기적인 신호이건 아니건, 모든 신호에 대해 적용할 수 있는 변환 방법이다. 반면에 푸리에 급수는 주기적
infograph.tistory.com
02-1. 푸리에 급수: 사인파의 표현 방법(사인함수, 각속도, 라디안) https://infograph.tistory.com/224
02-1. 푸리에 급수: 사인파의 표현 방법(사인함수, 각속도, 라디안)
앞 챕터에서 주기적인 신호를 표현하기 위한 가장 단순한 함수로 '사인 함수'를 후보로 해서 알아봤다. 사실 지금까지의 신호 이론은 '모든 신호는 단순한 신호의 조합으로 나타낼 수 있고, 이
infograph.tistory.com
02-2. 푸리에 급수: 사인파의 합을 통해 복잡한 파형 만들기 https://infograph.tistory.com/240
02-2. 푸리에 급수: 사인파의 합을 통해 복잡한 파형 만들기
앞장에서 "모든 신호는 단순한 신호의 조합으로 나타낼 수 있고, 이 단순한 신호는 사인파로 나타낼 수 있다"라고 했고, 사인파를 나타내는 방법을 알아봤다. 이제 실제로 사인파들을 합쳐서 복
infograph.tistory.com
03. 푸리에 계수 https://infograph.tistory.com/242
03. 푸리에 계수
앞 장에서 복잡한 신호를 여러 사인파의 합으로 나타내는 푸리에 급수를 알아봤다. $ y(t) = a_0 + \sum _{n=1}^{\infty}{a_n \cos 2\pi nft + b_n \sin 2\pi nft} $ [식 1] $ y(t) = a_0 + \sum _{n=1}^{\infty}{..
infograph.tistory.com
04. 푸리에 급수의 복소지수 표현 https://infograph.tistory.com/246
04. 푸리에 급수의 복소지수 표현
푸리에 급수의 사인 함수 표현, 복소 지수 표현은 아래와 같다. [푸리에 급수의 사인함수 표현] $y(t) = a_0 + \sum _{n=1}^{\infty}{a_n \cos n\omega t + b_n \sin n\omega t}$ $a_0 = \frac {1}{T} \int _{0}^{..
infograph.tistory.com
04-1. 복소 평면, 복소평면에서의 원 https://infograph.tistory.com/243
04-1. 복소 평면, 복소평면에서의 원
복소평면에서의 원 복소평면에서의 원에 대한 미분을 알아볼 것이다. 뜬금없을 수도 있으나, 이 글의 끝까지 가보면 왜 이것에 대해 알아보는지 이유를 알 수 있을 것이다. 이를 위해서 우리는
infograph.tistory.com
04-2. 복소 지수, 자연 상수 e https://infograph.tistory.com/244
04-2. 복소 지수, 자연 상수 e
앞에서 복소평면에서 반지름이 1인 원을 그리는 함수가 $C(x) = \cos x + i\sin x$ 임을 알아봤다. 이것이 $e^{i \theta}$와 같다는 것을 보이는 것이 최종 목표이고, 증명 방법은 사인과 코사인 함수로 표
infograph.tistory.com
04-3. 매클로린 급수, 오일러 공식 https://infograph.tistory.com/245
04-3. 매클로린 급수, 오일러 공식
앞 챕터들에서 복소평면에서의 원의 함수 식, 그리고 복소 지수함수와 그에 대한 미분에 대해 알아봤다. 원의 함수 식: $\cos x + i\sin x $ 복소 지수 함수: $e^{ix}$ 이제 이 둘이 만날 차례이다. 즉, 복
infograph.tistory.com
04-4 푸리에 급수를 복소지수로 표현하기 https://infograph.tistory.com/247
04-4 푸리에 급수를 복소지수로 표현하기
이번 챕터는 푸리에 급수를 복소지수 형태로 변환하는 과정을 볼 것이다. 즉, 아래와 같은 사인함수로 표현한 푸리에 급수식을 복소지수 형태로 바꾸는 것이다. [사인함수 표현] $y(t) = a_0 + \sum _{
infograph.tistory.com
04-5 푸리에 급수의 삼각함수 표현 vs. 복소지수 표현 https://infograph.tistory.com/270
04-5 푸리에 급수의 삼각함수 표현 vs. 복소지수 표현
이 장은 04-1 ~ 04-4까지의 내용을 정리하면서, 푸리에 급수의 두 표현방법(삼각함수, 복소지수함수)을 비교하고, 그 의미를 알아볼 것이다. 앞 장까지 우리가 알아봤던 것은 크게 2가지 였다. - 푸
infograph.tistory.com
04-6. 푸리에 급수 예제를 손으로 풀어보기 https://infograph.tistory.com/273
04-6. 푸리에 급수 예제를 손으로 풀어보기
앞 장까지 푸리에 급수에 대해 알아봤다. 푸리에 급수는 아래와 같은 식으로 표현되었다. 푸리에 급수의 삼각함수 표현 $$ \begin{align} &y(t) = a_0 + \sum _{n=1}^{\infty}{(a_n \cos n\omega t + b_n \sin n\o..
infograph.tistory.com
05. 푸리에 변환, 푸리에 역변환 (Fourier Transform, Inverse Fourier Transform) https://infograph.tistory.com/271
05. 푸리에 변환, 푸리에 역변환 (Fourier Transform, Inverse Fourier Transform)
이번 장에서 드디어 앞 장에서 설명했던 푸리에 급수를 이용해서 푸리에 변환식을 유도해 낼 것이다. 앞 장에서 푸리에 급수에 대해 알아봤다. 푸리에 급수의 복소지수 표현은 아래와 같았다. $$
infograph.tistory.com
05-1. 푸리에 변환식의 의미 https://infograph.tistory.com/272
05-1. 푸리에 변환식의 의미
앞 장에서 푸리에 급수에서부터 푸리에 변환으로 식을 유도해 냈다. $$ Y(f)=\int _{-\infty} ^{\infty} {y(t)e^{-i2 \pi ft} dt} \quad :푸리에\: 변환 \tag{식 1}$$ $$y(t)=\int _{-\infty} ^{\infty} {Y(f)e^{i..
infograph.tistory.com
05-2. 한 신호를 정해서 손으로 푸리에 변환 해보기 https://infograph.tistory.com/283
05-2. 한 신호를 정해서 손으로 푸리에 변환 해보기
간단한 신호(시간에 대한 크기 값으로 주어지는)에 대해서 푸리에 변환을 해보자. 직접 손으로 한 번 풀어봐야, 푸리에 변환식의 의미를 체감하게 될 것이다. 푸리에 변환식에는 적분이 들어가
infograph.tistory.com
06. 이산신호에 대한 푸리에 변환 https://infograph.tistory.com/284
06. 이산 푸리에 변환 (DFT, Discrete Fourier Transform)
지금까지 다뤘던 푸리에 변환은 연속신호에 대한 변환이었다. 연속 시간에 대한 신호와 연속된 주파수에 대한 변환이었다. 연속 시간이라는 것은 시간과 시간 사이에 빈틈이 없다는 것이다. 주
infograph.tistory.com
06-1. 이산시간 푸리에 변환(DTFT, Discrete Time Fourier Transform) https://infograph.tistory.com/322
06-1. 이산시간 푸리에 변환(DTFT, Discrete Time Fourier Transform)
시간은 드문드문한 '이산시간'으로, 주파수는 연속으로 가정해서 푸리에 변환하는 것이다. 앞에 챕터 5까지는 연속시간 및 연속주파수를 기준으로 해서 푸리에 변환을 했고, 이것이 푸리에 변환
infograph.tistory.com
06-2. 이산 푸리에 변환(DFT, Discrete Fourier Transform) https://infograph.tistory.com/323
06-2. 이산 푸리에 변환(DFT, Discrete Fourier Transform)
앞 페이지에서 이산 시간 푸리에 변환(DTFT)까지 유도했고, 이제 주파수까지 이산인 이산 푸리에 변환(DFT)을 유도해본다. 시간을 '이산'으로 만드는 것은, 어떤 아날로그 신호에 대해서 연속된 시
infograph.tistory.com
06-3. DFT의 수식 이해 https://infograph.tistory.com/325
06-3. DFT의 수식 이해
앞 페이지까지 DFT의 수식이 어떻게 유도되는지 알아봤고, 그 수식은 다음과 같다. $$ DFT: \; \; Y(k)=\sum_{n=0}^{N-1}{y(n)e^{-i\frac{2\pi}{N}kn}}, \; \; 0\leq k < N \tag {1} $$ $$ IDFT: \; \; y(n) = \fr..
infograph.tistory.com
06-4. 엑셀을 이용한 DFT 계산(1/4) https://infograph.tistory.com/326
06-4. 엑셀을 이용한 DFT 계산(1/4)
어떤 신호값에 대해 실제로 DFT 및 IDFT 계산을 해보면 수식의 의미를 더 깊게 이해할 수 있다. 앞 페이지에서 아주 간단한 형태의 가상 신호값을 이용해서 DFT 계산을 해봤는데, 이렇게 간단한 값
infograph.tistory.com
06-5. 엑셀을 이용한 DFT 계산(2/4) https://infograph.tistory.com/327
06-5. 엑셀을 이용한 DFT 계산(2/4)
이번 페이지에서는 정현파에 대한 신호값을 생성하고, 이 신호값에 대한 DFT를 엑셀을 이용해서 수작업으로 계산해볼 것이다. (수작업이라고 표현한 이유는, 엑셀에 내장되어 있는 FFT함수를 써
infograph.tistory.com
06-6. 엑셀을 이용한 DFT 계산(3/4) https://infograph.tistory.com/328
06-6. 엑셀을 이용한 DFT 계산(3/4)
예제 3. 주파수 1 kHz 파형에 대한 DFT 계산 예제3에 대한 엑셀 자료는, 엑셀파일 "DFT예제_3.xlsm"의 Sheet "3" 참조. 엑셀파일은 이 페이지 제일 밑에 보면 있음 앞의 예제에서는 코사인 파형 1개 주기에
infograph.tistory.com
06-7. 엑셀을 이용한 DFT 계산(4/4) https://infograph.tistory.com/329
06-7. 엑셀을 이용한 DFT 계산(4/4)
[예제 4] N값을 크게 해서 주파수 분해능을 높이기 두 개의 코사인 파가 합쳐진 신호를 가지고 분석해 볼 것이다. 신호 수식: 1 kHz와 1.1kHz의 정현파가 합쳐진 신호 --> $\cos{2\pi \cdot 1000t} + \cos{2\pi \c.
infograph.tistory.com
07. FFT (Fast Fourier Transform, 고속 푸리에 변환) https://infograph.tistory.com/331
07. FFT (Fast Fourier Transform, 고속 푸리에 변환)
앞에서 살펴봤던 DFT의 수식을 그대로 이용해서, 실제 신호에 대한 푸리에 변환을 하기에는 무리가 있다. 계산량이 너무 많기 때문이다. $$ DFT: \; \; Y(k)=\sum_{n=0}^{N-1}{y(n)e^{-i\frac{2\pi}{N}kn}}, \; \;..
infograph.tistory.com
07-1. FFT의 유도 https://infograph.tistory.com/332
07-1. FFT 유도
이 페이지에서는 DFT를 고속 계산하게 해 주는 쿨리-튜키 알고리즘을 소개한다. 쿨리-튜키 알고리즘은 분할정복(Divide and Conquer)기반 알고리즘이다. 분할정복은 $O(N^2)$의 계산량을 $O(N\log{N})$으로
infograph.tistory.com
07-2. FFT 예제를 손으로 풀어보며 이해하기 https://infograph.tistory.com/342
07-2. FFT 예제를 손으로 풀어보며 이해하기
$y(n)={0,0,0,0,1,1,1,1}$인 값에 대해 FFT 수식을 이용해서 단계별로 손으로 문제를 풀듯이 계산해보자. 먼저 이 값을 DFT 수식을 이용해서 엑셀에서 구해보면 다음과 같다. $$ DFT: \; \; Y(k)=\sum_{n=0}^{N-1}..
infograph.tistory.com
07-3. 엑셀에서 FFT 계산하기 (엑셀 자체 FFT 기능) https://infograph.tistory.com/343
07-3. 엑셀에서 FFT 계산하기 (엑셀 자체 FFT 기능)
엑셀에는 FFT 계산을 할 수 있는 기능이 있다. 디폴트 기능으로 오픈되어 있는 것은 아니고, 사용할 수 있도록 몇 가지 설정을 하면 FFT 계산을 할 수 있다. 엑셀에서 FFT 기능 활성화 하기 1. 엑셀
infograph.tistory.com
07-4. 엑셀에서 직접 FFT 프로그래밍 작성하기 https://infograph.tistory.com/344
07-4. 엑셀에서 직접 FFT 프로그램 만들기
이 페이지에서는 엑셀 VBA를 이용해서 FFT 프로그래밍을 하는 것을 설명할 것이다. 사실 엑셀에서 FFT 프로그래밍을 직접 한 것은 구글링을 해봐도 별로 없다. 없다는 것은 다 그 이유가 있는데, 가
infograph.tistory.com
[07-4] Fastest FFT code for Excel VBA https://infograph.tistory.com/351
[07-4 Code] Fastest FFT code for Excel VBA
This page explain FFT program made for Excel VBA. It is no limit of input data size, therefore you can calculate over 4096 size data and it will perform very fast. FFT Execution time in the Excel by..
infograph.tistory.com
07-5. 가장 빠른 Java용 FFT 구현해보기 https://infograph.tistory.com/349
07-5. 가장 빠른 Java용 FFT 구현해보기
이 페이지는 Java로 구현하는 FFT, 그것도 수행 속도를 빠르게 하는 것에 목적을 둔 프로그래밍 코드를 소개한다. 전체 소스코드는 여기 참조 앞 페이지에서 엑셀로 만드는 FFT의 경우는, 속도는 느
infograph.tistory.com
[07-5] Fastest FFT code for Java https://infograph.tistory.com/350
[07-5 Code] Fastest FFT code for Java
This page introduce very fast FFT code for Java. It will execute FFT calculation for 64 kBytes input data in 10ms. Execution result of Test_FFFT class ** test_simple_fft ** 8.0, 0, -2.0+4.82842712..
infograph.tistory.com
07-6. Java로 FFT 알고리즘 충실히 구현하기 https://infograph.tistory.com/352
07-6. Java로 FFT 알고리즘 충실히 구현하기
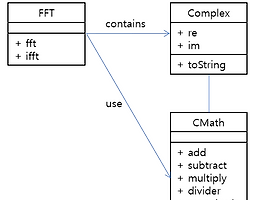
이번 페이지에서는 FFT 알고리즘을 Java 언어의 특성을 충실히 살리면서, 읽을 수 있는 수준의 알고리즘 구현을 해보고자 한다. Java 언어의 특성을 살린다는 의미는, 복소수의 표현을 Complex라는 객
infograph.tistory.com
[07-6 Code] FFT program for Java https://infograph.tistory.com/354
[07-6 Code] FFT program for Java
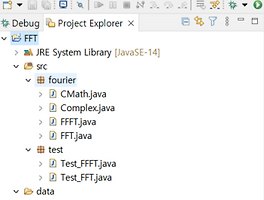
This page introduce FFT sourece code. There are 4 java soure file and 1 text file. - fourier/FFT.java - fourier/Complex.java - fourier/CMath.java - test/Test_FFT.java - data/input.txt 1. fourier/..
infograph.tistory.com
07-7. C로 짠 FFT Code https://infograph.tistory.com/357
07-7. C로 짠 FFT Code
C나 C++로 된 FFT 코드는 예전부터 많이 있을 것이기에, C용 FFT 코드는 잘 되어 있는 코드를 소개만 하려고 했었다. 그러나, 여러 코드들을 구글링해서 찾아봤으나, 예상외로 맘에 드는 코드를 찾지
infograph.tistory.com
[07-7 Code]FFT source code for C https://infograph.tistory.com/358
[07-7 Code]FFT source code for C
1. fft.h int fft(long N, double XR[], double XI[]); char * cplxStr(double re, double im); 2. fft.c /* fft.c */ /* 2022.8.7 Created by HJ */ #include #include #define PI 3.14159265358979 int fft(long..
infograph.tistory.com
'푸리에 변환, 신호 > 푸리에 변환의 모든 것' 카테고리의 다른 글
| [07-7 Code]FFT source code for C (0) | 2022.08.07 |
|---|---|
| 07-7. C로 짠 FFT Code (1) | 2022.08.07 |
| [07-6 Code] FFT program for Java (0) | 2022.08.06 |
| 07-6. Java로 FFT 알고리즘 충실히 구현하기 (0) | 2022.08.05 |
| [07-5 Code] Fastest FFT code for Java (0) | 2022.08.05 |
