이 페이지에서는 엑셀 VBA를 이용해서 FFT 프로그래밍을 하는 것을 설명할 것이다.
사실 엑셀에서 FFT 프로그래밍을 직접 한 것은 구글링을 해봐도 별로 없다.
없다는 것은 다 그 이유가 있는데, 가장 큰 이유는 굳이 따로 프로그래밍할 필요가 없다일 것 같다.
속도도 느린 엑셀 VBA를 이용해서 굳이 FFT를 해야 할 일도 없겠고, 또한 엑셀 자체로 FFT 함수가 있으니깐.
그렇지만, 내게는 다음과 같은 작성 이유가 있다.
- 신호 데이터를 분석하거나 할 때 엑셀만큼 좋은 툴이 없다. 해서, FFT도 엑셀에서 바로 수행하고, 그 결과 데이터를 엑셀에서 분석하면서 인사이트를 얻고 하면 좋겠다.
- 근데, 엑셀에 있는 FFT 함수는 4096개 데이터가 한계다. 그 이상의 데이터는 처리할 수 없다. 4096으로는 너무 적다. 더 큰 데이터에 대해서도 FFT가 가능한 것이 필수다.
엑셀 VBA로 해도 그다지 느리지 않게 FFT를 짤 수 있다. 엑셀 VBA가 느린 것은 Worksheet를 이용하면서 화면 전환을 할 때 가장 느려지는 것이다. 데이터 자체를 배열로 처리해서 프로그래밍하면 Java 정도의 속도는 나오게 할 수 있다. (물론 C 만큼은 아니지만)
엑셀에서의 FFT 프로그래밍은 2019년 5월에 작성해서 다른 사이트에 올린 바 있다.
우리나라에서는 별로 없지만, 전 세계로 보면, 가끔 엑셀에서 4096 크기 이상의 데이터에 대한 FFT 수행 필요가 있는 사람이 있고, 가끔 자신의 PC에서 동작이 안된다는 메일이 있었으나, 시간이 없어서 잘 대응을 못했다.
이번에 짧게 여유가 생겨 이번 기회에 좀 보완하고, 여기에 그 코드를 남기고자 한다.
아래는 Reddit에서 언급된 내용
https://www.reddit.com/r/excel/comments/r0i4vd/fft_analsis_with_much_greater_than_4096_points_of/
화면 디자인
FFT를 수행하기 위한 화면은, 엑셀의 기본 FFT 화면과 유사하게 하는데, 더 심플하게 작성한다.
- 입력 셀과 출력 셀만 물어보자
- 입력 데이터가 2의 지수승개가 아니어도 자동 패딩 하도록 하자 (엑셀 내장 FFT에서는 데이터의 개수가 2의 지수승이 아니면 에러)
아래와 같이 디자인 했다.

기본 아키텍처
복소수 처리
엑셀 VBA의 데이터 타입에는 복소수가 없고, 복소수를 처리하는 함수도 없다.
Workbook 함수에는 복소수의 연산 함수가 있어서, VBA에서 Workbook 함수를 호출하는 형태로 프로그래밍할 수도 있으나, Workbook함수를 호출하는 것은 엑셀 버전에 따른 호환 문제도 있을 수 있고, 복소수 연산 함수를 만드는 것이 그리 복잡한 일도 아니기에, 그냥 자체로 만들기로 한다.
'complexNumModule'에 복소수 관련 함수를 만들어 모아 놓는다.
Option Explicit
Public Type Complex
re As Double
im As Double
End Type
Public Function Cplx(ByVal real As Double, ByVal imaginary As Double) As Complex
Cplx.re = real
Cplx.im = imaginary
End Function
Public Function CAdd(ByRef z1 As Complex, ByRef z2 As Complex) As Complex
CAdd.re = z1.re + z2.re
CAdd.im = z1.im + z2.im
End Function
Public Function CSub(ByRef z1 As Complex, ByRef z2 As Complex) As Complex
CSub.re = z1.re - z2.re
CSub.im = z1.im - z2.im
End Function
Public Function CMult(ByRef z1 As Complex, ByRef z2 As Complex) As Complex
CMult.re = z1.re * z2.re - z1.im * z2.im
CMult.im = z1.re * z2.im + z1.im * z2.re
End Function
Public Function CDivR(ByRef z As Complex, ByVal r As Double) As Complex
' Divide complex number by real number
CDivR.re = z.re / r
CDivR.im = z.im / r
End Function
Public Function CMagnitude(ByRef z As Complex) As Double
CMagnitude = Sqr((z.re ^ 2) + (z.im ^ 2))
End Function
Public Function String2Complex(ByVal s As String) As Complex
Dim sLen As Integer
Dim re As Double, im As Double
s = Trim(s)
sLen = Len(s)
If sLen = 0 Then: GoTo ERROR_HANDLE
'support a+aj style
If InStr(s, "j") Then
s = Replace(s, "j", "i")
End If
'total cases: (1){a, -a} (2){-a+bi +a+bi} {-a-bi +a-bi} {-bi +bi} (3){a+bi, a-bi, bi}
Dim pos As Integer
If InStr(s, "i") = 0 Then ' (1){a, -a}
re = CDbl(s)
im = 0
ElseIf InStr(s, "+") = 1 Or InStr(s, "-") = 1 Then '(2){-a+bi +a+bi} {-a-bi +a-bi} {-bi +bi}
pos = InStr(2, s, "+")
If pos > 0 Then '-a+bi +a+bi
re = CDbl(Mid(s, 1, pos - 1))
im = CDbl(Mid(s, pos + 1, sLen - pos - 1))
Else
pos = InStr(2, s, "-")
If pos > 0 Then '-a-bi +a-bi
pos = InStr(2, s, "-")
re = CDbl(Mid(s, 1, pos - 1))
im = CDbl(Mid(s, pos, sLen - pos))
Else ' -bi +bi
re = 0
im = CDbl(Left(s, sLen - 1))
End If
End If
Else '(3){a+bi a-bi, bi}
pos = InStr(s, "+")
If pos > 0 Then 'a+bi
re = CDbl(Mid(s, 1, pos - 1))
im = CDbl(Mid(s, pos + 1, sLen - pos - 1))
Else 'a-bi bi
pos = InStr(s, "-")
If pos > 0 Then 'a-bi
re = CDbl(Mid(s, 1, pos - 1))
im = CDbl(Mid(s, pos, sLen - pos))
Else 'bi
re = 0
im = CDbl(Left(s, sLen - 1))
End If
End If
End If
String2Complex = Cplx(re, im)
Exit Function
ERROR_HANDLE:
String2Complex = Cplx(0, 0)
End Function
속도 향상 기법
엑셀 VBA 작성 시 가장 속도 향상을 보일 수 있는 방법이, 셀 데이터를 직접 사용하지 않고 배열로 전환 후 사용하는 것이다.
예를 들어, 셀의 어떤 범위 rangeA와 rangeB 간의 합성곱을 해야 한다면, 일반적으로는 rangeA와 rangeB의 값을 하나씩 읽어내면서 계산을 하게 되는데, 이렇게 해서는 속도가 너무 느리게 된다. 엑셀 VBA에서 가장 느린 연산이 셀의 데이터를 읽고 쓰는 연산이기 때문이다.
속도를 빠르게 하기 위해서는, 이 rangeA와 rangeB의 데이터를 배열로 한 번에 저장하고, 그 배열 데이터를 이용해서 연산을 하게 하면 된다.
수행 속도를 빠르게 하는 여러 기법이 사용되었으나, 위의 배열을 이용한 연산을 적용함으로써, 64 kBytes 데이터에 대해서도 FFT를 1초 이내에 수행 가능하도록 할 수 있었다.!!
엑셀 자체 FFT의 경우 4 kBytes(4096)개 데이터에 대해서만 하더라도 FFT 계산에 수십 초 걸린다.

대표적으로, 워크시트의 Range 데이터를 배열 객체로 변환하는 코드는 다음과 같다.
' read the first row value in the range and return it as double value array
Public Function Range2Array(r As Range) As Double()
Dim i As Long, size As Long
Dim arr() As Double
size = r.Rows.Count
ReDim arr(0 To size - 1) As Double
For i = 1 To size
arr(i - 1) = r(i)
Next i
Range2Array = arr
End Function
FFT 알고리즘 구현
FFT 계산을 위한 알고리즘은, 앞 페이지에서 다뤘던 쿨리-튜키 알고리즘을 사용한다. 분할 정복 알고리즘이다.
$$ \begin{align}Y(k) = P(k) + W^kQ(k), \; &0 \le k \le {\frac{N}{2}-1} \\ Y(k+\frac{N}{2})=P(k)-W^kQ(k), \; &0 \le k \le {\frac{N}{2}-1} \tag{1} \end{align} $$
(식 2)에서,
- $P(k)$: 짝수항에 대한 데이터. 분할 정복에 의해 하위단 신호 데이터에서부터 차근차근 계산되는 값
- $Q(k)$: 홀수항에 대한 데이터
- $W^k$: Convolution Ring값. k값만으로도 계산 가능
합성곱 링(Convolution Ring) W 계산
W값은 입력 데이터인 y(n) 값의 개수가 주어지기만 하면 계산할 수 있다.
y(n)의 개수가 N개이면 0~$\frac{N}{2}-1$까지의 W를 계산해두고 사용하면 된다.
$$ \begin{align} W^k &= e^{-i\frac{2\pi}{N}k} \\ &=\cos{\frac{2\pi}{N}k}-i\sin{\frac{2\pi}{N}k} \; &0 \le k \le {\frac{N}{2}-1} \end{align} $$
속도를 조금이라도 빠르게 하려면, 이 W 값을 미리 계산해서 코드에 담아두고 써도 된다.
만약 65536개의 데이터까지만 FFT 계산을 허용한다면, 32768개의 W를 미리 계산해서 코드에 배열로 담아두고 사용하면 된다.
그러나, 이 코드에서는 그렇게 하지 않았다. 데이터의 개수에 제한을 두고 싶지 않고, W를 계산하는데 N/2번의 사인 함수 계산만이 필요하기에, 속도에 심각한 영향을 주지 않을 것이기 때문이다.
이 코드에서는 'CalculateW' 라는 함수를 만들어서 W를 계산하고 나서, 이 W를 이용해서 FFT를 계산하도록 했다.
' calculate convolution ring W
' W[k] = cos(theta) - isin(theta)
' theta = (2pi*k/N)
Function CalculateW(cnt As Long, isInverse As Boolean) As Complex()
Dim arr() As Complex
Dim i As Long
Dim T As Double, theta As Double
Dim N As Long, N2 As Long
N = cnt
N2 = N / 2
ReDim arr(0 To N2 - 1) As Complex 'enough to calculate 0 to (N/2 -1)
T = 2 * myPI / CDbl(N)
If isInverse Then
For i = 0 To N2 - 1
theta = -(T * i)
arr(i) = Cplx(Cos(theta), -Sin(theta))
Next i
Else
For i = 0 To N2 - 1
theta = T * i
arr(i) = Cplx(Cos(theta), -Sin(theta))
Next i
End If
CalculateW = arr
End Function그리고 또 하나의 특징은(속도 향상을 위한), W의 계산을 N이 달라질 때마다 재계산하지 않는다는 것. 즉, Bottom-up으로 FFT를 계산해 나갈 때, N=2 -> 4 -> 8 -> 16 ... 이렇게 증가하게 되는데, 이때마다 W를 재계산하지 않는다는 것이다.
예를 들어 y(n)의 개수가 8인 데이터에 대해 계산한다면,
- $W_8^k$에 해당하는 4개의 W를 구한다. $\{ W_8^0, W_8^1, W_8^2, W_8^3\}$
- 1단계: N=2일 때이고, 0번째 원소만 사용 --> $W_8^0$
- 2단계: N=4일 때이고, {0번째, 2번째} 원소만 사용 --> $\{ W_8^0, W_8^2 \}$
- 3단계: N=8일 때이고, {0번째, 1번째, 2번째, 3번째} 원소 모두 사용 --> $\{ W_8^0, W_8^1, W_8^2, W_8^3\}$
이렇게되는 원리는 W의 식에 값을 대입해보면 알 수 있다. N=8의 경우 $W_8^k = e^{-i\frac{2\pi}{8}k}$ 이기에,
- N=2의 경우: $W = e^{-i\frac{2\pi}{2}k}$이고, 0에서 $\frac{N}{2}-1$까지의 W에 대해 e의 지수부만을 표시해보면, $\{-i\pi \cdot 0 \} = \{ 0 \}$ --> 즉, $W_8^0$
- N=4의 경우: $W = e^{-i\frac{2\pi}{4}k}$이고, 0에서 $\frac{N}{2}-1$까지의 W에 대해 e의 지수부만을 표시해보면, $\{ -i\frac{\pi}{2} \cdot 0, -i\frac{\pi}{2} \cdot 1 \} = \{ 0, -i\frac{\pi}{2}\}$ --> $\{W_8^0, W_8^2\}$
- N= 8의 경우는, --> $\{W_8^0, W_8^1, W_8^2, W_8^3\}$
분할 정복(Divide and Conquer) 코드 작성
분할정복 알고리즘을 구현하는 방법은 크게 2가지로 나눌 수 있다. 하나는 재귀 호출(Recursion)을 이용하는 것이고, 다른 하나는 Bottom up 방법.
재귀 호출을 사용하면, 알고리즘 수식을 그대로 프로그래밍만 하면 되기에 코딩이 좀 편하나, 재귀 호출하는 횟수가 많아지면 스택 메모리가 부족해서 에러가 발생할 수 있고, 무엇보다 Bottom up 방법보다 속도가 느리다. 이는 재귀 호출이 함수를 여러 번 호출하는 구조이기에, 이전 함수 데이터를 저장하고 새로운 함수를 호출하는 반복 과정에서 속도 저하가 있을 수밖에 없기 때문이다.
따라서, 여기서는 Bottom up 방법을 사용했다.
Bottom up 방법은 신호 데이터인 y(n)에서부터 시작해서 쭈욱 위쪽으로 계산해가면서 끝내 Y(k)를 구해나가는 방법이다.
가장 밑 단에서는 y(n) 데이터 2개씩 해서 DFT값을 구하고, 그다음 4개씩에 대한 DFT를 구하고, 그다음 8개에 대한 DFT값을 구해나가면서, 끝내는 Y(k)를 구하는 방법이다.
여기서 문제는, 처음 시작하는 y(n) 데이터의 2개씩 쌍을 어떻게 결정하는가이다.
N=8일 때, y(n)에 대한 쌍은 다음과 같다.
(0,4) (2,6) (1, 5) (3,7)
맨 위쪽 Y(k)에 대해서 생각해보면, {0,1,2,3,4,5,6,7}에서 그 밑단에서 짝수항과 홀수항으로 나누면 {0,2,4,6} {1,3,5,7}로 구분되고, 이를 다시 짝수항과 홀수항으로 나누면, {0,4} {2,6} {1,5} { 3,7}로 되기 때문이다.

N=16일 때는 다음과 같다.
(0,8) (4,12) (2,10) (6,14) (1,9) (5,13) (3,11) (7, 5)
따라서, Bottom up으로 계산할 때는, y(n)의 데이터를 이러한 순서로 2개씩 해서 DFT값을 구하면서, 위쪽으로 올라가야 한다.
y(n) 데이터의 이러한 순서를 알아내는 것은, 순서를 나타내는 값을 이진수로 나타낸 후, 그 이진수의 값을 뒤집은 상태에서 정렬하면, 신기하게도 이러한 순서대로 된다.
8의 경우를 보면,
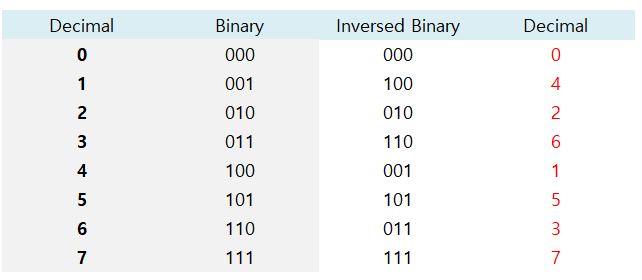
16의 경우를 보면,
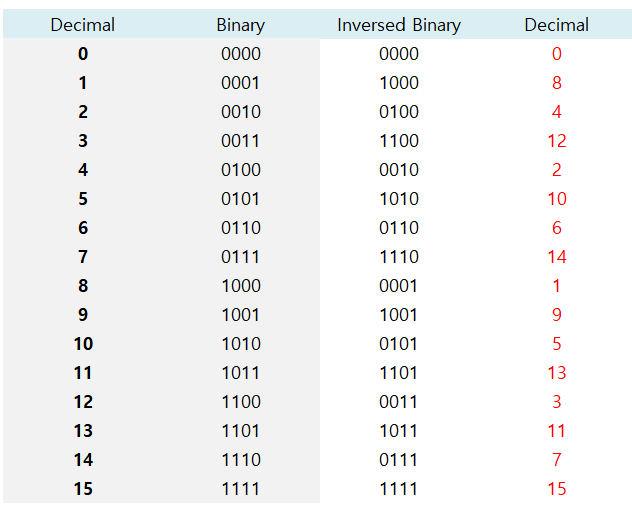
따라서, 프로그램 코드에서는, y(n)의 순서를 위와 같은 규칙에 맞게 구한 후, 그 순서의 데이터에 대해서 2개씩 계산하면 된다.
아래 코드는 위의 규칙으로 y(n) 데이터의 순서를 조정하는 코드이다.
Function ArrangedNum(num As Long, numOfBits As Integer) As Long
Dim arr() As Byte
Dim i As Integer, j As Integer
Dim k As Long
If (2 ^ numOfBits) <= num Then GoTo EXIT_FUNCTION
'1) Decimal number -> Reversed Binary array : (13,4) -> {1,1,0,1} -> {1,0,1,1}
ReDim arr(0 To numOfBits - 1) As Byte
For i = 0 To numOfBits - 1
j = (numOfBits - 1) - i
k = Int((num / (2 ^ j)))
arr(j) = (k And 1)
Next i
'2) Reversed Binary -> Decimal: {1,0,1,1} -> 1*2^3 + 0*2^2 + 1*2&1 + 1 = 11
Dim d As Long
For i = 0 To numOfBits - 1
d = d + (arr(i) * 2 ^ (numOfBits - 1 - i))
Next i
ArrangedNum = d
Exit Function
EXIT_FUNCTION:
ArrangedNum = 0
End Function
' rangeArr[1 to n, 1]
Function arrangeToFFTArray(arr() As Complex, size As Long, numOfBits As Integer) As Complex()
Dim i As Long, j As Long
Dim arrangedArr() As Complex
ReDim arrangedArr(0 To size - 1) As Complex
For i = 0 To size - 1
j = ArrangedNum(i, numOfBits) '{000,001,010, 011, 100, 101, 110, 111} -> {0, 4, 2, 6, 1, 5, 3, 7}
arrangedArr(j) = arr(i)
Next i
arrangeToFFTArray = arrangedArr
End Function
최종 FFT 및 IFFT 값 계산
IFFT를 구하는 것도 FFT와 동일한 원리이기에, FFT_Forward라는 공통 함수를 만들고, IFFT와 FFT를 구할 때 공통으로 사용하도록 했다.
코드에서 핵심은, 데이터에 대해서 2개짜리 FFT, 4개짜리 FFT, ... 이처럼 Bottom-up으로 해가면서, FFT의 공식을 적용해나가는 부분이다.
아래 코드를 보면, For 루프에서 RegionFFT를 호출하는 부분이 그 부분이다.
For curLoop = 0 To totalLoop - 1
tgtIdx = (tgtIdx + 1) Mod 2
srcIdx = (tgtIdx + 1) Mod 2
regionSize = 2 ^ (curLoop + 1) ' if N=8: 2 -> 4 -> 8
kJump = 2 ^ (totalLoop - curLoop - 1) ' if N=8: 4 -> 2 -> 1
i = 0
Do While i < N
Call RegionFFT(X, srcIdx, tgtIdx, i, regionSize, kJump, W)
i = i + regionSize
Loop
Next curLoop
RegionFFT에서 실제 FFT 공식이 적용되는데, 이때 미리 구해둔 W(k)를 활용하는 부분과, 복소수 처리하는 2차원 배열 X[2][N-1] 하나만을 이용해서, X[0]과 X[1]이 각 단계별로 한 번은 source가 되었다가, 다시 한번을 target이 되었다가 하면서 메모리를 아끼며 사용하는 부분이, 이 부분 코드의 특징이다. (이렇게 함으로써 메모리 공간 절약 및 속도 개선됨)
' X({0,1}, [0,n-1]): 2d array. (0, n) <--> (1,n)
' src: src index of the array. 0 or 1
' tgt: tgt index of the array. 1 or 0
' s : starting index of the data in the array
' size: region size to be calculated
' kJump : k's jumping value
' W(0 ~ n-1) : Convolution ring
Sub RegionFFT(X() As Complex, src As Integer, tgt As Integer, _
s As Long, size As Long, kJump As Long, W() As Complex)
Dim i As Long, e As Long
Dim half As Long
Dim k As Long
Dim T As Complex
' Xm+1[i] = Xm[i] + Xm[i+half]W[k]
' Xm+1[i+half] = Xm[i] - Xm[i+half]W[k]
k = 0
e = s + (size / 2) - 1
half = size / 2
For i = s To e
T = CMult(X(src, i + half), W(k))
X(tgt, i) = CAdd(X(src, i), T)
X(tgt, i + half) = CSub(X(src, i), T)
k = k + kJump
Next i
End Sub
코드 수행
코드 수행을 해보면 64 kBytes의 꽤 큰 데이터에 대해서도 1초 이내에 FFT 수행된다.!!!!
아래는 무려 64 kBytes의 데이터에 대해 FFT를 해보는 영상이다. 화면 녹화를 하고 있어서 CPU 부하가 좀 걸려서 1초가 약간 넘는 1040ms 정도 소요되는 것을 볼 수 있는데, 일반적으로 1초 이내에 끝난다.
아래는 각 데이터 사이즈에 대한 수행 소요시간이다.
| 데이터 개수 | FFT 수행 속도(화면 출력 포함) [ms] |
| 4 kB | 62 |
| 8 kB | 115 |
| 16 kB | 235 |
| 64 kB | 984 |
엑셀 내장된 FFT 기능을 사용한 경우 4 kBytes 데이터가 한계이고, 4 kBytes에 대한 FFT 수행이 약 6초(데이터에 따라서 좀 가변)정도 소요되는 것과 비교하면, 이 페이지에서 소개한 FFT 방식이 얼마나 빠른 건지 느낄 수 있을 것이고, 이 정도면, 엑셀에서도 충분히 FFT를 수행하면서 분석할 수 있을 것이다.
여기서 소개한 FFT 프로그램이 전부 완벽하게 들어 있는 엑셀파일: 쓸데없이 무단 배포되는 것을 막기위해 파일암호화를 해놨습니다. 필요하신 분은 파일 다운로드 받은 후, 이 글의 댓글 혹은 이메일로 암호를 요청하시면 보내드립니다. (이메일 주소: p14jeffwest@gmail.com )
파일 암호는: 2.718282
- 끝 -
| 이전글: 07-3. 엑셀에서 FFT 계산하기 (엑셀 자체 FFT 기능) |
| 다음글: 07-5. 가장 빠른 Java용 FFT 구현해보기 |
| 다다음글: [07-5] Fastest FFT code for Java |
'푸리에 변환, 신호 > 푸리에 변환의 모든 것' 카테고리의 다른 글
| 07-5. 가장 빠른 Java용 FFT 구현해보기 (2) | 2022.08.05 |
|---|---|
| [07-4 Code] Fastest FFT code for Excel VBA (0) | 2022.08.05 |
| 07-3. 엑셀에서 FFT 계산하기 (엑셀 자체 FFT 기능) (0) | 2022.07.28 |
| 07-2. FFT 예제를 손으로 풀어보며 이해하기 (5) | 2022.07.28 |
| 07-1. FFT 유도 (9) | 2022.07.25 |


