| 푸리에 변환을 바로 설명하기 전에 푸리에 급수부터 파악해볼 것이다. 푸리에 변환은 주기적인 신호이건 아니건, 모든 신호에 대해 적용할 수 있는 변환 방법이다. 반면에 푸리에 급수는 주기적인 신호에만 적용될 수 있는 방법이다. 주기적인 신호가 어떻게 푸리에 급수로 표현될 수 있는 지 보고, 이를 확장해서 푸리에 변환을 알아볼 것이다. 알아보기 순서: 푸리에 급수(주기) --> 푸리에 변환(비주기로 확장) |
주기적인 신호
주기적인 신호는 일정한 시간 간격으로 똑같은 값을 가지는 신호이다.
아래는 1초마다 값을 읽은 신호이다. 신호의 값이 보이는 패턴을 보면, 5초마다 같은 패턴을 보인다. 즉, 5초마다 같은 값을 가지고 있고, 이러한 것을 주기적인 신호라 한다.
$$ f(t) = f(t + 5) $$
1초마다 띄엄띄엄 값이 존재하는 것이 아니라, 연속적으로 값이 존재하는 신호에 대해서도 마찬가지다. 일정 시간 간격으로 똑같은 값이면 주기 신호다.
| 일정 시간 간격에만 값이 존재하는 신호를 이산 신호(Discreat-time Signal)라 하고, 연속해서 값이 존재하는 신호를 연속신호(Continuout-time Signal)라 한다. 일반적으로, 이산 신호의 값은 대괄호 [ ]를 써서 나타내고, 연속신호는 괄호( )를 사용한다. 예를 들어 이산 신호 A의 첫 번째 값은 A[1], 두 번째 값은 A[2] 연속신호에 대해서 10초일 때의 값은 A(10), 12초일 때의 값은 A(11) |
주기 신호가 일정한 시간 간격마다 똑같은 값을 가진다는 것을 수학적으로 표현하면,
주기가 N인 이산 신호의 경우는,
$$ {A[n]} = {A[n+N]} $$
주기가 T인 연속 신호의 경우는,
$$ {A(n)} = {A(n+T)} $$
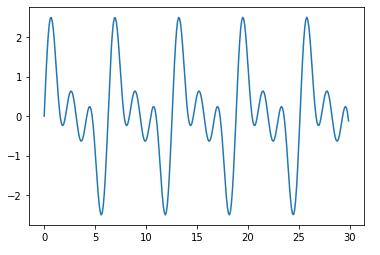
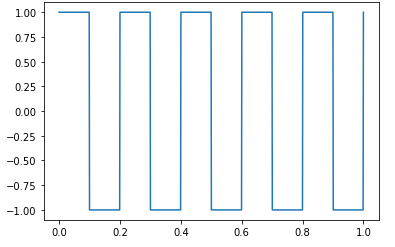
다음과 같은 신호 모두 주기적 신호이다.
이 그래프는 파이썬으로 그린 것으로, 소스는 여기서 확인할 수 있음
(이 소스는 필자가 직접 작성한 파이썬 소스코드입니다. ^^)
푸리에 급수는 어떤 '주기적인 신호'를 '단순한 주기 신호'들의 합으로 나타내는 것이다.
여기서 '단순한 주기 신호'를 어떻게 표현할까?
먼저 '단순한 주기 신호'를 수식으로 표현할 수 있는 적당한 함수를 찾아야겠다. (수식으로 표현하려는 이유는, 그래야만 그 신호에 대해 수학적인 기법들을 써서 더하거나 빼거나 하는 등의 연산을 할 수 있기 때문이다. )
...
우리가 알고 있는 수학 함수 중에 주기성을 띈 함수는 어떤 게 있을까?
주기 함수이려면 다음 조건을 만족해야 한다.
$$ {f(x)} = {f(x+T)} $$
어떤 $x$값에 대한 값과, 그 $x$에 주기 T만큼 더한 $x$+T에서의 값이 같아야 한다.
당연히 $ y=2x $ 같은 선형 함수는 주기 함수가 아니다. $x=1$에서 $y=2$인데, $x$를 아무리 증가시켜도 다시 $y=2$인 곳이 나타나지 않는다.
...
삼각함수가 대표적인 주기 함수다.
$ \sin x $, $ \cos x $, $ \tan x $ 이러한 삼각함수는 주기 함수이다.
$ \sin x $와 $ \cos x $는 360도마다, $ \tan x $는 180도마다 같은 값이 돌아오는 주기성을 가진다.
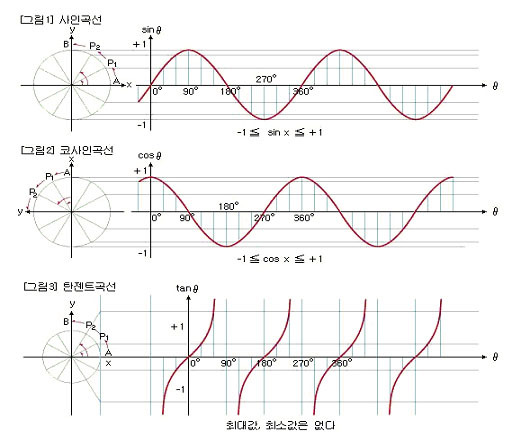
그렇다면 일단 sine 함수를, 어떤 단순한 주기 함수로 삼고, 이 sine함수를 이용해서 모든 주기 함수를 표현할 수 있는지 확인해보도록 하자.
| 실제로 푸리에 급수는 삼각함수의 사인과 코사인 함수를 이용해서 모든 주기함수를 나타낸다. 이 과정을 차근차근 알아볼 것이다. |
삼각함수
삼각형의 오른쪽 아랫각이 직각, 왼쪽 아랫각이 $ \theta $일 때, 아래 그림과 같이 된다.
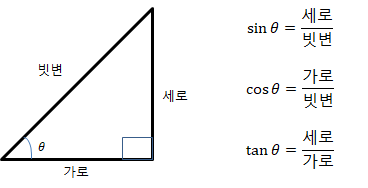
빗변과 세로의 관계를 $\sin \theta $, 빗변과 가로를 $ \cos \theta $, 가로와 세로를 $ \tan \theta $로 나타낸 것이라 생각하면 된다.
즉, 이러한 삼각형에서 $ \theta $값이 같다면 각 변 간의 비례가 같다는 것이다.
예를 들어, 아래와 같은 삼각형이 있을 때, $ \theta $를 가만히 두고 빗 변 c를 2배로 늘리면 a와 b는 어떻게 될까를 생각해보자.
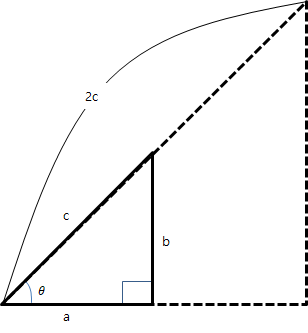
답은, 밑변인 가로는 2a가 되고, 세로는 2b가 된다.
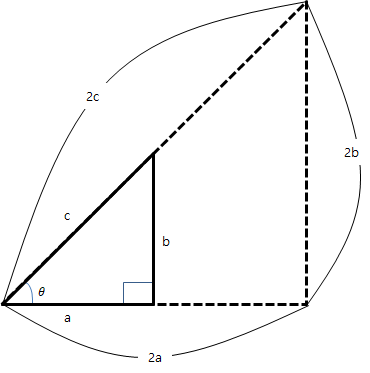
c가 절반으로 줄어들면 a와 b도 절반으로 줄어든다.
즉, c : a : b의 관계가 $ \theta $가 변하지 않는 한 바뀌지 않는 것이다.
따라서, c와 a, c와 b, a와 b의 관계 값이 $ \theta $에 의해 바뀌는 것이고, 이러한 값을 $ \sin \theta $, $ \cos \theta $, $ \tan \theta $라고 이름 붙인 것이다.
| 여기서 주의깊게 생각할 것은, sin cos tan 이라는 기호가 어떤 약속이라는 점이다. 삼각형에서 두 변 사이의 관계를 나타내는 약속. 즉, 두 변 사이의 크기 비율이, 각 하나에 의해 결정된다는 것을 표현하려는 약속이라는 점이다. $\sin \theta$는 빗 변과 세로 변 사이를 $\cos \theta$는 빗 변과 가로 변 사이의 비를 표현하기 위한 약속 기호인 것이다. |
사인 곡선
고등학교 때 이미 $ \sin \theta $의 그래프가 다음과 같이 된다는 것을 배웠을 것이다.
원점에서 $0$이고, $2 \pi $를 주기로 해서 커브를 그리는.
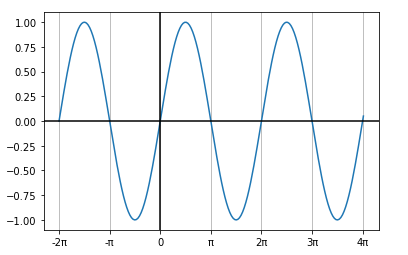
사인 함수의 그래프가 왜 이렇게 되는지 생각해보자.
...
사인 함수의 정의에 의하면 $ \sin \theta = {세로/빗변}$이다.
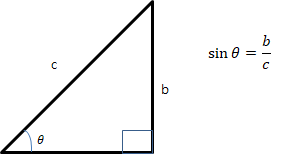
계산을 간단히 하기 위해서 빗변 c를 1로 놓으면 $ \sin \theta = b$라고 할 수 있다.
이제 반지름이 1인 원을 그리고, 원점에서 원둘레 위의 임의의 점 p로 선을 그리고, x축과 그 직선 사잇각을 $ \theta $라 하면, $ \sin \theta $는, 삼각형의 높이에 해당하고, 그 값은 그 임의의 점 p의 y좌표 값이 될 것이다. (왜냐면 $ \sin \theta = 높이 / 빗변 $이고 여기서 빗변=1 이기 때문)
$ \theta = 0 $일 때의 p는, 가로 선인 x축과 원이 만나는 점이다. 정확하게는 원의 오른편 둘레와 x축이 만나는 점.
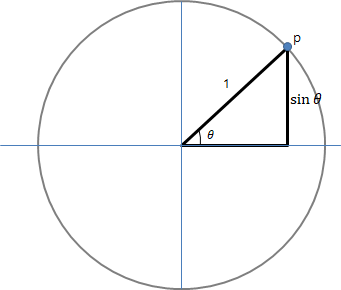
이 p를 원둘레를 따라 반시계 방향으로 점점 움직이면, $ \theta $ 값이 점점 커질 것이고, $ \sin \theta $의 값도 점점 커지면서 $ \theta = 90도$일 때 최대 값 1이 될 것이다.
좀 더 p를 이동시키면, $ \sin \theta $는 점점 작아지다가 $ \theta = 180도 $에서 0(zero)이 될 것이다.
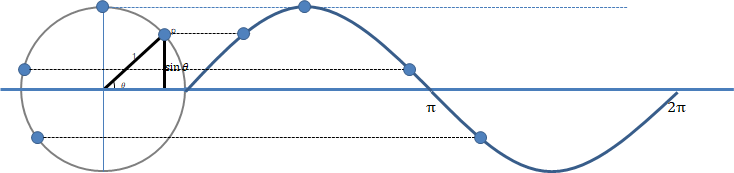
이렇게 점 p를 이동시키면서 그때의 $ \sin \theta $의 값을 그려보면 아래와 같이 된다.
(이 동영상은 파이썬 코드로 필자가 직접 만든 동영상입니다.)
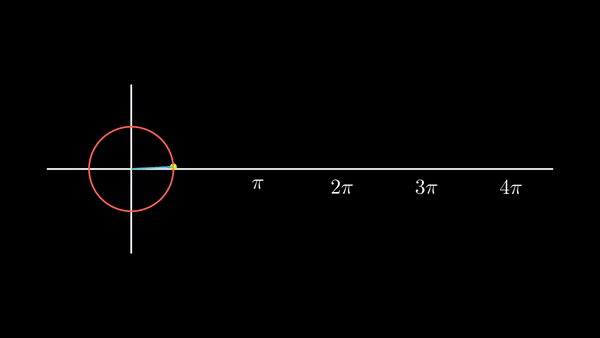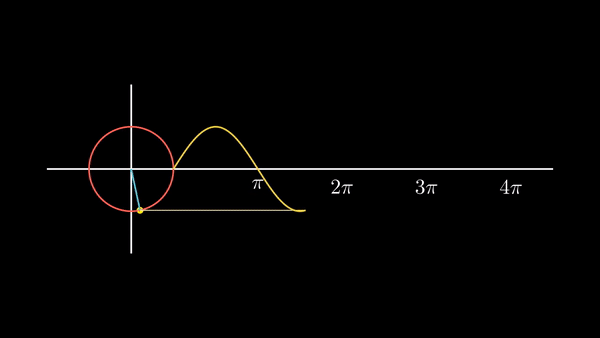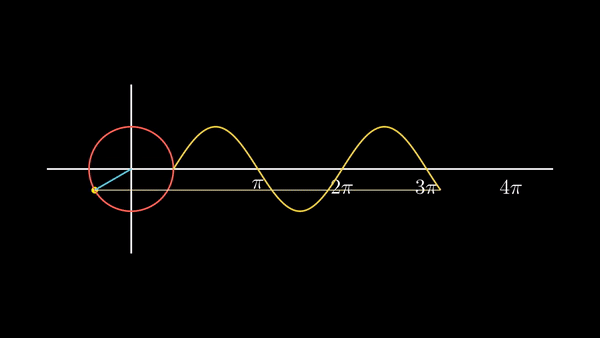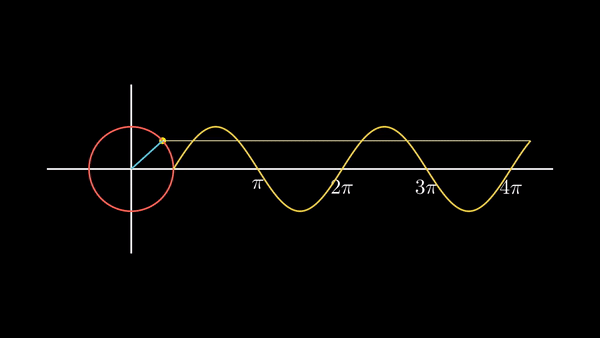
| 사인 곡선이라는 것이, 원 운동을 하는 어떤 점의 '세로 값의 변화'라는 것을 기억해 두자. |
코사인 곡선
코사인 함수의 그래프는 아래와 같이 표현된다.
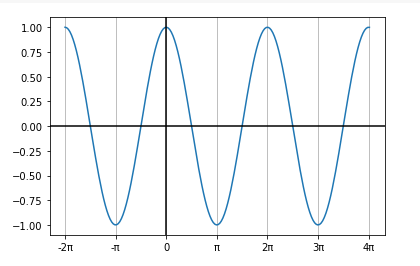
사인 그래프와 모양이 비슷한데, 0에서의 값이 다르다. 사인 함수에서는 값이 0인데, 코사인에서는 1이다.
근데 자세히 보면, 코사인 그래프는 사인 그래프를 왼쪽으로 $ \pi / 2 $ (=90도) 이동시킨 것이라 할 수 있다. 즉,
$$\cos {(-90도)} = \sin {(0도)} = 0$$
$$ \cos {(0도)} = \sin {(90도)} = 1도 $$
일반화하면,
$$ \cos \theta = \sin (\theta + 90도) = \sin (\theta + \pi / 2)$$
...
코사인 그래프도 위의 사인 그래프를 그리는 원리로 생각해보면, 반지름이 1 짜리인 원에서 밑변의 크기가 $ \cos \theta $가 됨을 알 수 있다.
$ \theta = 0 $일 때 $ \cos \theta = 1 $이고, 점 p가 반시계 방향으로 돔에 따라 $ \theta $가 점점 커지면서 $ \cos \theta $ 값은 점점 작아져서, $ \theta = 90도$일 때 0(zero)이 된다.
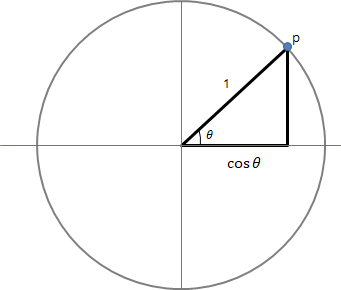
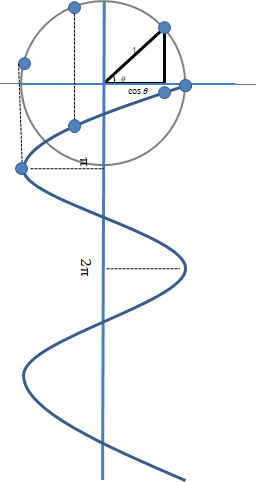
밑변의 크기를 나타내야기에, 좌표계에서 x 축 길이에 해당하고, 따라서 그래프를 아래 방향으로 늘려서 진행해가면서 그 x축 길이값을 나타낸 것이다.
...
원 상의 점이 이동함에 따라 코사인 그래프와 사인 그래프를 동시에 그려보면 아래와 같이 될 것이다.
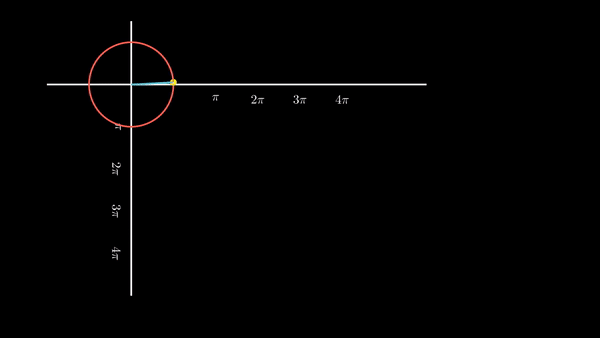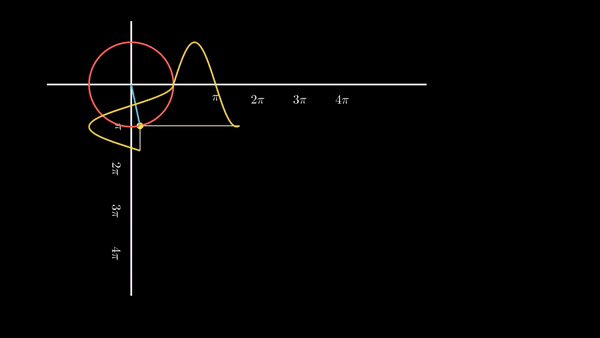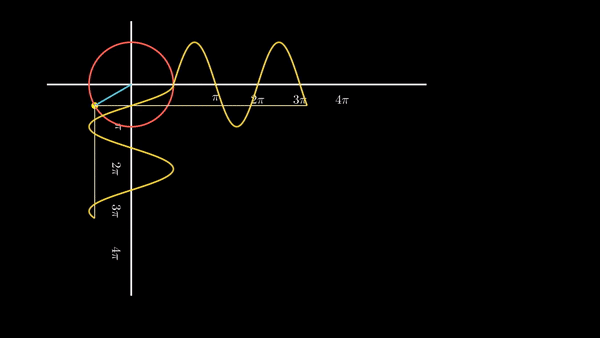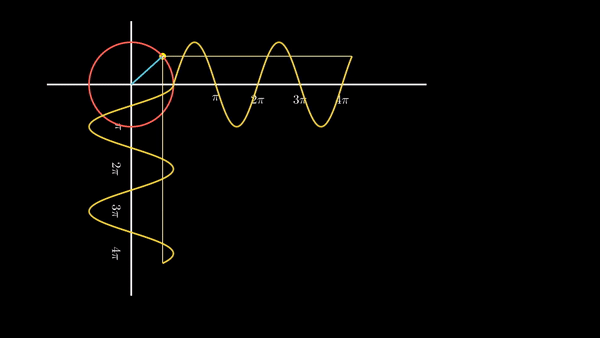
| 원 운동을 하는 점의 높이 값의 변화가 사인 함수, 밑변 값의 변화가 코사인 함수인 것이다. |
사인 함수와 코사인 함수에 대해 정리해 보면,
- $\sin \theta$는 $\theta$값에 따른 빗변과 높이의 비율이다. (위에서 봤던 반지름 1짜리 원을 머릿속으로 생각해 보자). 따라서, $\theta=0$ 일 때는 0이고 (높이가 0이니깐), $ \theta$가 커질 수로 조금씩 커지다가 $\theta =90도$일 때 최댓값이 된다.
- $\cos \theta$는 $\theta$값에 따른 빗변과 밑변의 비율이다. 따라서, $\theta=0$에서 1이고 (원 그림에서 생각해보면, 밑변이 1이니깐), $\theta$가 커질수록 조금씩 작아지고 $\theta =90도$ 일 때 0이 되고, $\theta = 180도$ 일 때 -1이 된다.
가장 간단한 주기 함수로 사인과 코사인 함수를 택했고, 이 사인/코사인 함수에 대해 알아봤다.
다음 챕터에서는 이 사인/코사인 함수에 수학적인 연산을 적용해서 복잡한 주기 함수를 표현할 수 있는지 알아볼 것이다.
-끝-
| 이전글: 푸리에 변환이란 |
| 다음글: 02-2. 푸리에 급수: 사인파의 표현 방법(사인함수, 각속도, 라디안) |
| 다음다음글: 02-3. 푸리에 급수: 사인파의 합을 통해 복잡한 파형 만들기 |
'푸리에 변환, 신호 > 푸리에 변환의 모든 것' 카테고리의 다른 글
| 04. 푸리에 급수의 복소지수 표현 (0) | 2020.10.11 |
|---|---|
| 03. 푸리에 계수 (7) | 2020.10.04 |
| 02-2. 푸리에 급수: 사인파의 합을 통해 복잡한 파형 만들기 (4) | 2020.10.01 |
| 02-1. 푸리에 급수: 사인파의 표현 방법(사인함수, 각속도, 라디안) (8) | 2020.10.01 |
| 01. 푸리에 변환이란 (4) | 2020.09.12 |
