반응형
1. fft.h
int fft(long N, double XR[], double XI[]);
char * cplxStr(double re, double im);2. fft.c
/* fft.c */
/* 2022.8.7 Created by HJ */
#include <math.h>
#include <stdio.h>
#define PI 3.14159265358979
int fft(long N, double XR[], double XI[]){
/* 1. check 2^n count -> if else then return -1 */
if ((N !=0) && ((N & (N-1)) != 0) ) return -1;
/* 2. calculate W */
long N2 = N >> 1;
double WR[N2], WI[N2]; /* Real and Imaginary part */
double T = 2 * PI / N;
for(long i=0;i<N2;++i){
WR[i] = cos(T*i);
WI[i] = -sin(T*i);
}
/* 3. shuffle input array index to calculate bottom-up style FFT */
int log2N = (int)log2(N);
double tmp;
for(long n=1;n<N-1;++n){
long m = 0; /* reversed num of n*/
for(int i=0;i<log2N;++i){
m |= ((n >> i) & 1) << (log2N-i-1); /* reverse the bits */
}
if(n<m){ /* exchange */
tmp = XR[n];
XR[n] = XR[m];
XR[m] = tmp;
}
}
/* 4. execute fft */
for(int loop=0; loop<log2N; ++loop){
long regionSize = 1 << (loop+1); /* if N=8: 2 -> 4 -> 8 */
long kJump = 1 << (log2N - loop - 1); /* if N=8: 4 -> 2 -> 1 */
long half = regionSize >> 1;
for(register long i=0; i<N; i += regionSize){
long blockEnd = i + half -1;
long k=0;
double TR, TI;
for(register long j=i; j<=blockEnd; ++j){ /* j start from i */
TR = WR[k] * XR[j+half] - WI[k] * XI[j+half];
TI = WI[k] * XR[j+half] + WR[k] * XI[j+half];
XR[j+half] = XR[j] - TR;
XI[j+half] = XI[j] - TI;
XR[j] = XR[j] + TR;
XI[j] = XI[j] + TI;
k += kJump;
}
}
}
return 0;
}
char * cplxStr(double re, double im){
static char s[50];
if(re==0 && im==0){
sprintf(s,"0");
}else if(re == 0) {
sprintf(s,"%.12fi",im);
}else if(im == 0) {
sprintf(s,"%.12f",re);
}else if(im > 0) {
sprintf(s,"%.12f + %.12fi",re,im);
}else {
sprintf(s,"%.12f - %.12fi",re,-im);
}
return s;
}
3. test_fft.c
#include <stdio.h>
#include <time.h>
#include <math.h>
#include "fft.h"
int test_simple(void){
const long N=8;
double XR[8]= {0,0,0,0,1,1,1,1};
double XI[8];
printf("** test_simple_fft **\n");
int result = fft(N,XR, XI);
for(long i=0; i<N; ++i) printf("%s, ", cplxStr(XR[i],XI[i]));
printf("\n");
return 0;
}
#define CNT 65536
#define PI 3.14159265358979
int test64k(void){
long N = CNT;
static double XR[CNT]; //use heap not stack avoiding "Segmentation Fault" for over 1M data
static double XI[CNT];
printf("** test_measure_time **\n");
for(long i=0;i<N;++i){
XR[i] = cos(2*PI*0.004*i);
}
double beforeT, diffT;
int result=-1;
beforeT = clock();
result=fft(N, XR, XI);
diffT = clock() - beforeT;
printf("%.0fms\n", diffT);
if(result < 0){
printf("FFT calculation Error\n");
}
for(long i=0;i<8;++i) printf("%s ,",cplxStr(XR[i],XI[i]));
printf("\n");
for(long i=(N-8);i<N;++i) printf("%s ,",cplxStr(XR[i],XI[i]));
return 0;
}
int main(){
test_simple();
test64k();
return 0;
}Compile and Link
gcc -o test_fft -g fft.c test_fft.c
Execution Result of test_fft
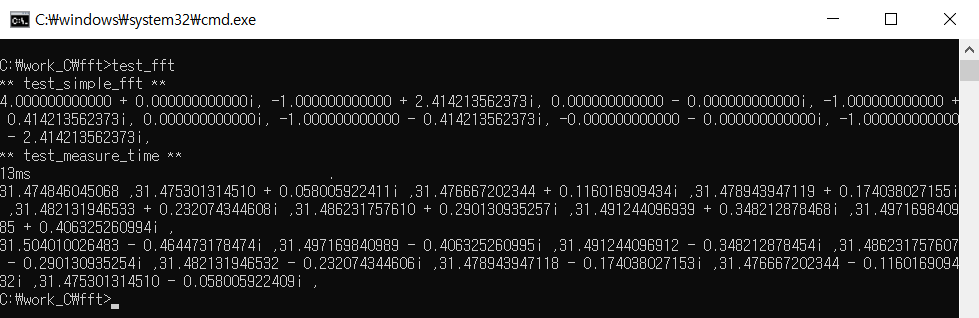
소스 파일
fft.c
0.00MB
fft.h
0.00MB
test_fft.c
0.00MB
- The End -
반응형
'푸리에 변환, 신호 > 푸리에 변환의 모든 것' 카테고리의 다른 글
| [목차]푸리에 변환의 모든 것 (12) | 2022.08.07 |
|---|---|
| 07-7. C로 짠 FFT Code (1) | 2022.08.07 |
| [07-6 Code] FFT program for Java (0) | 2022.08.06 |
| 07-6. Java로 FFT 알고리즘 충실히 구현하기 (0) | 2022.08.05 |
| [07-5 Code] Fastest FFT code for Java (0) | 2022.08.05 |