간단한 신호(시간에 대한 크기 값으로 주어지는)에 대해서 푸리에 변환을 해보자. 직접 손으로 한 번 풀어봐야, 푸리에 변환식의 의미를 체감하게 될 것이다.
푸리에 변환식에는 적분이 들어가 있어서, 신호가 조금만 복잡해도 손으로 풀기 어렵다. 해서, 가장 단순한 신호를 가지고 계산해보자.
가장 단순한 신호. 계속해서 1의 값을 가지는 신호를 대상으로 하자.
시간에 대한 그래프로 그려보면 아래와 같이 될 것이다.

이러한 신호에 대한 주파수 영역에서의 그래프는 어떻게 될까?
시간이 변함에 따라 신호 값의 변화가 없이 계속 1이다. 즉, 시간에 대한 변화값이 없다는 것은 주기가 무한대라는 얘기이고, 주파수는 0이라는 것.
따라서, 주파수가 0인 부분에서만 값이 존재하게 될 것이다.

이제 (그림 1)과 같은 신호에 대해 푸리에 변환을 해서, 진짜 (그림 2)와 같은 변환이 되는지 확인해 보자.
푸리에 변환식을 다시 적어본다.
$$ Y(f)= \int _{-\infty} ^{\infty} {f(t)e^{-i2\pi ft}dt} \tag {1}$$
흠... 문제는 적분의 범위가 $-\infty$ ~ $\infty$이다. 무한대에 대한 계산을 할 수 없다.
그렇다면, 계산이 가능하게 하기 위해 임의로 시간의 범위 $\Delta t$를 정해보자. (일단 계산 가능한 범위를 정해서 계산해보고, 이 $\Delta t$를 점점 더 커지게 해서 무한대까지 키우는 걸로 해보는 게 풀이 전략)
$\Delta t$의 범위를 0을 중심으로 좌우 대칭이 되게 하자. 그래야 계산이 편할 것이다. 범위는 $-\dfrac {\Delta t}{2}$ ~ $\dfrac {\Delta t}{2}$

이렇게하면, $t < -\dfrac{\Delta t}{2}$와 $t > \dfrac {\Delta t}{2}$의 영역에서는 신호 값이 없고(=신호 값이 0이고), $-\dfrac {\Delta t}{2}$와 $\dfrac {\Delta t}{2}$ 사이에서만 값이 존재하게 된다. 따라서, 이를 그래프로 다시 그려보면 아래와 같은 모습이 된다.

이제 (그림 4)와 같은 신호를, 식 (1)을 이용해서 푸리에 변환 해보자.
적분의 범위는 $-\dfrac {\Delta t}{2}$와 $\dfrac {\Delta t}{2}$ 사이만 될 것이다. 그 이외의 범위에서는 값이 $0$이기 때문이다. 그리고, $y(t)$의 값은 $1$이다.
이제 식 (1)을 다시 써보면,
$$ \begin{align} Y(f) &= \int _{-\frac {\Delta t}{2}} ^{\frac {\Delta t}{2}} {1 \cdot e^{-i2\pi ft}}dt \\ &= \left [ \dfrac{-1}{i2\pi f} e^{-i2\pi ft} \right ]^{\frac {\Delta t}{2}} _{-\frac{\Delta t}{2}}\\ &= - \dfrac {1}{i2\pi f}\left ( e^{-i2\pi f\cdot \frac {\Delta t}{2}}-e^{-i2\pi f \cdot \frac {-\Delta t}{2}} \right ) \\ &= - \dfrac {1}{i2\pi f} ( e^{-i\pi f\cdot \Delta t}-e^{i\pi f \cdot \Delta t} ) \\ &=\dfrac {1}{i2\pi f} (e^{i\pi f \cdot \Delta t} -e^{-i\pi f \cdot \Delta t}) \end{align} \tag {2}$$
여기서 지수함수의 적분 방법이 쓰였는데, 적분 공식은 아래와 같다. 아래 식에서 $a$는 식 (2)에서는 $-i2\pi f$인 것이다.
$$ \int {e^{ax}}dx = \dfrac{1}{a} e^{ax} \tag {지수함수의 적분 공식}$$
푸리에 변환을 해봤더니 식 (2)가 나왔다. 아직 이 식을 가지고 어떤 값을 가지는지 유추하기 쉽지 않다. 복소 지수 때문인데, 이 복소 지수 식을 사인 함수 식으로 바꿔보자. 오일러 공식을 쓰면 되겠다.
$$ e^{i\theta} = \cos {\theta} + i\sin {\theta} \\ e^{-i\theta} = \cos {\theta} - i\sin {\theta} \tag {오일러 공식}$$
식 (2)에서 $\theta =\pi f\Delta t$로 놓고 다시 쓰면,
$$ \begin {align} Y(f) &= \dfrac {1}{i2\pi f}(e^{i\theta} - e^{-i\theta}) \\ &= \dfrac {1}{i2\pi f}(\cos \theta + i\sin \theta -(\cos \theta - i\sin \theta) )\\ &= \dfrac {1}{i2\pi f}(2i\sin \theta) \\ &= \dfrac {1}{\pi f} \sin \theta = \dfrac {\sin {(\pi f \Delta t})}{\pi f} \end{align} \tag {3}$$
사인 함수로 바꿔보니 식 (3)과 같이 나왔다. 근데, 이 식도 바로 이용할 수는 없겠다. 왜냐면, $f=0$일 때의 값을 구해야는데(우리가 처음에 미리 예측하길 $f=0$에서 값이 있을 것이라고 예상했었다.), 식 (3)에서 $f$의 위치가 분모에 있어서 $f=0$으로 넣으면 분모가 $0$이 되어 계산할 수가 없다. (0으로 나누는 것은 불능이기에)
어떻게 할까?
삼각함수의 극한에서, 아래와 같은 성질이 있다.
$$ \lim _{x \rightarrow 0} {\dfrac {\sin x}{x}} = 1 \tag {삼각함수의 극한 정리}$$
위와 같이 되는 것은 분모와 분자에 대해 각각 미분을 해보면 쉽게 증명이 된다.
$$\begin {align} \lim _{x \rightarrow 0} {\frac {\sin x}{x}} & = \lim _{x \rightarrow 0} {\dfrac {\frac{\mathrm{d} }{\mathrm{d} x}\sin x}{\frac{\mathrm{d} }{\mathrm{d} x}x}} \\ &= \lim _{x \rightarrow 0} \frac {\cos x} {1} \\ &= \frac {1} {1} = 1 \end{align} $$
식 (3)을 삼각함수의 극한 성질을 이용할 수 있는 형태로 바꿔보자. $\dfrac {\Delta t}{\Delta t}$를 곱해주면 되겠다.
$$\begin {align} Y(f) &= \dfrac {\sin {(\pi f \Delta t})}{\pi f} \\ &= \dfrac {\sin {(\pi f \Delta t})\cdot \Delta t}{\pi f \Delta t} \end{align} \tag {4}$$
식 (4)에서 $\pi f\Delta t \rightarrow 0$으로 보내면 $\dfrac {\sin {\pi f\Delta t}}{\pi f\Delta t}=1$이 되겠다. 근데, 이 식에서 변수는 $f$이기에, $f$에 대해서만 생각하면, $\pi f\Delta t \rightarrow 0$은 $f \rightarrow 0$과 똑같다. 따라서, $f \rightarrow 0$으로 보내는 것으로 해서 식 (4)를 전개하면,
$$ \begin {align} \lim _{f \rightarrow 0} Y(f) &= \lim _{f \rightarrow 0} \dfrac {\sin {(\pi f \Delta t})\cdot \Delta t}{\pi f \Delta t} \\ &= 1 \cdot \Delta t \\ & = \Delta t \end{align} \tag {5}$$
드디어 값이 나왔다.
푸리에 변환을 해봤더니, $f\rightarrow 0$일 때 $Y(f)=\Delta t$가 되었다.
여기서 $\Delta t$는 적분을 하는 구간 범위였다. 즉, $Y(f)$의 값은 적분을 하는 구간인 $\Delta t$가 되고, 적분을 하는 구간을 크게하면 할수록 $Y(f)$의 값이 커지는 것이다.
$\Delta t$의 값을 조금씩 변경시키면서 그래프를 그려보자. 식 (4)를 이용하겠다.
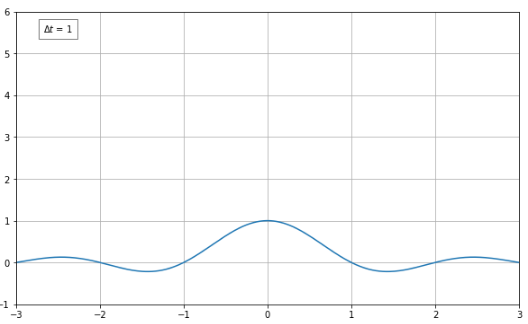
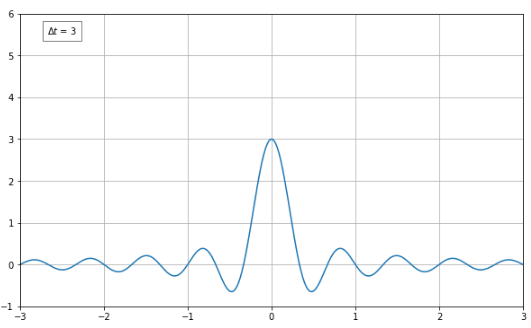
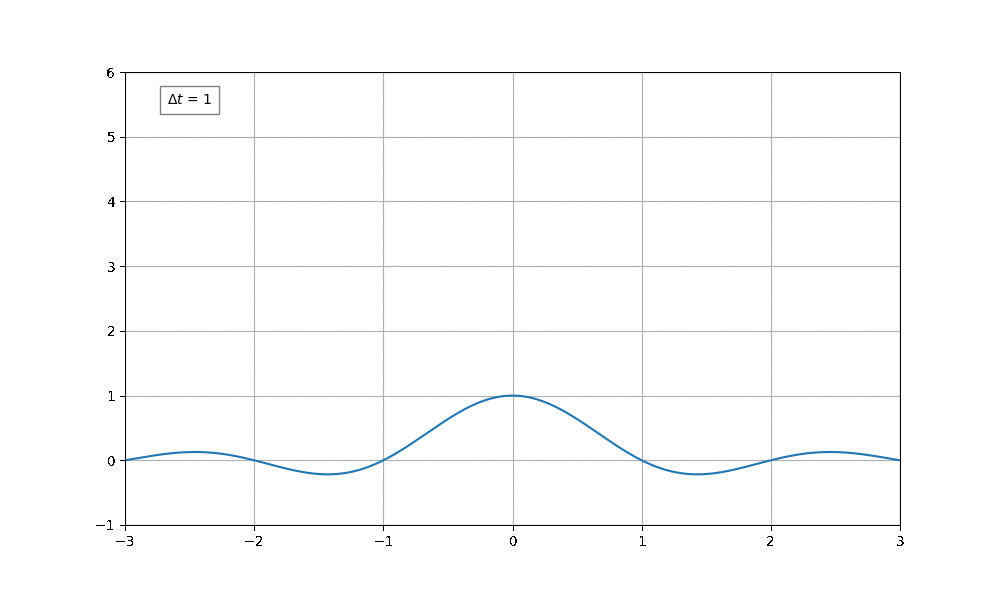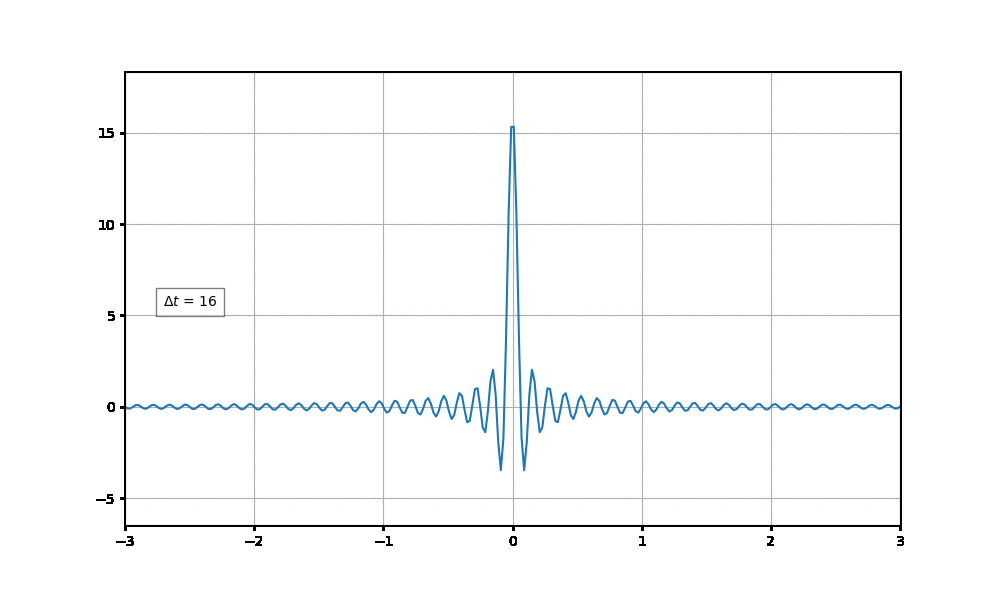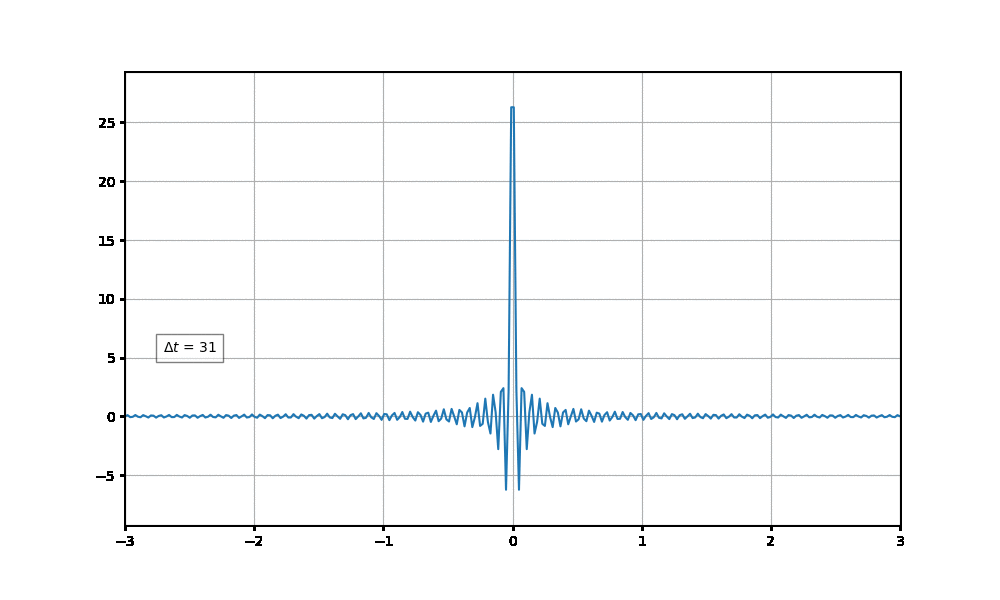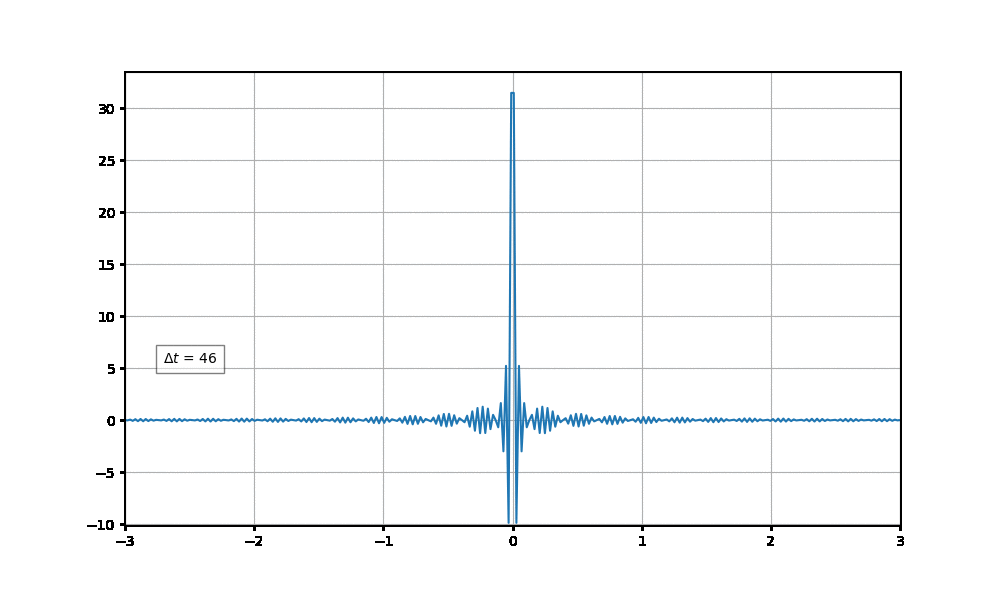
$\Delta t$의 값이 $1$일 때는 주파수가 0인 부분에서 좀 크긴하지만, 주파수가 0인 부분에서만 값이 존재할 것이라는 우리의 기대와는 다른 값이다. (우리는 처음부터 주파수가 0인 지점에서만 값이 존재할 것이라고 예상했었다.)
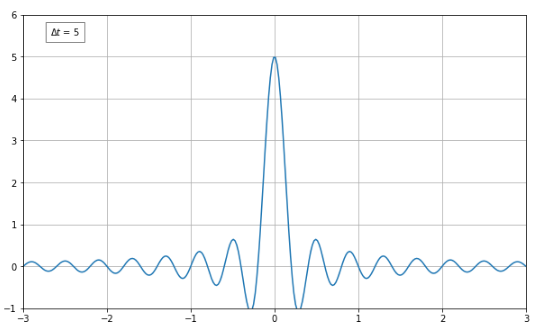
그러나 $\Delta t$의 값을 증가시켜가면, 점점 더 주파수가 0인 지점에서의 값이 커지고 있다.
$\Delta t$를 점점 더 증가시켜서 아주 큰 값이 되게해보자.
$\Delta t$가 아주 커지게 되면 주파수가 0인 부분에만 값이 남게 되겠다.
의미를 생각해보자.
먼저 $\Delta t=1$인 경우를 보면, 시간 간격을 매우 좁게 본 것이다. 원래는 무한대의 시간에 대해 계산을 해야 하는데, 아주 좁은 시간 영역만 보고, 그에 대한 주파수 성분을 유추해본 셈이다. 따라서, 무한대의 시간 간격을 가지고 봤을 때는 주파수가 0인 부분에만 값이 존재하겠지만, 적은 시간 간격의 정보만을 가지고 가지고 유추해보면 다른 주파수 성분도 있다는 오차가 발생하는 것이다.
여기서 주파수가 0인 부분 파형의 산의 너비를 $\Delta f$로 놓으면,
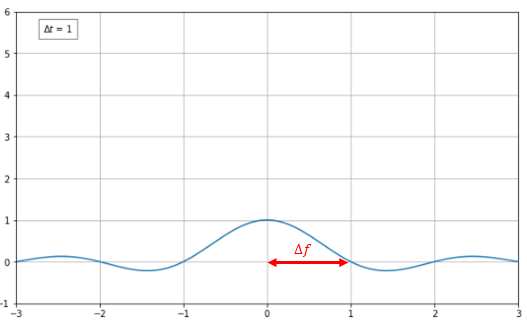
$\Delta t$의 값이 커질수록 $\Delta f$의 값이 작아지고, $\Delta t \rightarrow \infty$일 때는 $\Delta f \rightarrow 0$이 된다. 반대로 $\Delta t \rightarrow 0$이면 $\Delta f \rightarrow \infty$가 될 것이다.
$\Delta t \rightarrow \infty$ 이면 $\Delta f \rightarrow 0$
$\Delta t \rightarrow 0$ 이면 $\Delta f \rightarrow \infty$
이 처럼 $\Delta t$를 0으로 보내도, $\Delta f$를 0으로 보내도 두 값의 곱은 절대 0이 되지 않는다.
$$ \Delta t \times \Delta f \geq C \; , where \; C > 0 \tag {6}$$
식 (6)은 "입자의 위치와 운동량에 대한 정확한 값을 동시에 알 수 없다"는 '불확정성의 원리'와 닮아 있다.
(그림 4)에서 파동의 정확한 위치를 지정하기 위해 $\Delta t$를 줄이면, (그림 5)에서와 같이 정확한 주파수의 세기를 알 수 없었다.
푸리에 변환에 대해서 다시 생각해보자.
푸리에 변환은, 시간에 따라 '위치'가 변하는 파동 함수를, '운동량(세기)'이 다른 정현파의 합으로 표현하는 것이다.
여기서 정확한 '위치'를 한정하면 정확한 '운동량'을 알 수 없다.
즉, 푸리에 변환에서도 '불확정성의 원리'가 존재한다.
-끝-
| 이전글: 05-1. 푸리에 변환식의 의미 |
| 다음글: 06. 이산신호에 대한 푸리에 변환 |
| 다음다음글: 06-1. 이산시간 푸리에 변환(DTFT, Discrete Time Fourier Transform) |
'푸리에 변환, 신호 > 푸리에 변환의 모든 것' 카테고리의 다른 글
| 06-1. 이산시간 푸리에 변환(DTFT, Discrete Time Fourier Transform) (2) | 2022.07.05 |
|---|---|
| 06. 이산 푸리에 변환 (DFT, Discrete Fourier Transform) (0) | 2021.03.28 |
| 05-1. 푸리에 변환식의 의미 (0) | 2021.03.21 |
| 05. 푸리에 변환, 푸리에 역변환 (Fourier Transform, Inverse Fourier Transform) (6) | 2021.03.21 |
| 04-6. 푸리에 급수 예제를 손으로 풀어보기 (5) | 2021.03.21 |


