05-1. 푸리에 변환식의 의미

 

앞 장에서 푸리에 급수에서부터 푸리에 변환으로 식을 유도해 냈다. 

 

$$ Y(f)=\int _{-\infty} ^{\infty} {y(t)e^{-i2 \pi ft} dt} \quad :푸리에\: 변환 \tag{식 1}$$

$$y(t)=\int _{-\infty} ^{\infty} {Y(f)e^{i2\pi ft} df} \quad :푸리에\: 역변환 \tag{식 1-1}$$

 

푸리에 변환 (식 1)을 이용해서, 어떤 신호가 시간에 대한 함수(시간별로 그 파형의 크기가 주어지는)로 주어 졌을 때, 그 신호를 주파수에 대한 함수(각 주파수별 크기를 나타내는)로 표현할 수 있다. 아래 그림을 보자.

 

왼쪽의 시간에 대한 파형이 푸리에 변환에 의해 오른쪽의 주파수 파형으로 바뀔 수 있다. 그리고 반대로, 주파수 파형이 푸리에 역변환 식에 의해 왼쪽의 시간에 대한 파형으로 변환될 수 있는 것이다.

 

---

이 푸리에 변환식이 시간에 대한 파형을 주파수 파형으로 바꿀 수 있다는 것은 알겠는데, 과연 식의 어떤 점이 이런 역할을 할 수 있는 것일까? 

식에 대해 좀 더 알아보자.

 

(식 1)을 분해해보면,

• $Y(f)$ : 주파수에 대한 함수. 주파수 범위는 주파수로 나타낼 수 있는 전체 범위이며, 각 주파수별 크기 값이 표현될 수 있는 식이 되겠다. 즉, 어떤 주파수 $f$에 대해 그 크기를 알 수 있는 함수.
• $\int _{-\infty} ^{\infty} {X \cdot Y} dt$ : 모든 시간대에 대해서($-\infty$ ~ $\infty$) 어떤 $X$와 $Y$에 대한 곱을 한 것을 전부 합하는 것(적분하는 것). 여기서 $X$와 $Y$를 벡터로 본다면 두 벡터를 곱하는 내적($\vec X \cdot \vec Y$)으로 생각할 수 있다.
• 위에서 $X$로 나타낸 것은 원래의 신호 파형인 $y(t)$이고, $Y$는 복소평면에서 주파수 $f$이며 회전 방향이 음수(시계 방향)인 원의 식(=주파수 $f$이며 진행방향이 음의 방향인 사인파)

$e^{-iw\pi ft}$가 복소평면에서의 어떤 원에 대한 식이고, 이는 $cos$과 $sin$ 곡선으로 이루어지는 사인파의 표현과 똑같다는 것은 04-1. 복소 평면, 복소평면에서의 원에서 얘기한 바 있다. 헷갈린다면 그 부분을 다시 한번 보기 바람.

 

(식 1)을 분석해본 바를 의미 있게 해석해 보면 "어떤 주파수에 대한 푸리에 변환값은, 주어진 시간 파형과 어떤 주파수의 파형을 내적한 것의 합"이라고 할 수 있다.

 

이 말의 의미가 잘 안와닿을 수 있다.

예를 들어 설명해 보겠다.

 

---

예를 들어 어떤 시간에 대한 신호 $y(t)$가 있다고 했을 때, 이 신호의 주파수 $f=1$인 성분을 구해보도록 하자. 

 

(식 1)에 대입해 보면,

 

$$Y(1) = \int _{-\infty} ^{\infty} {y(t) \cdot e^{-i2\pi t} dt} \quad (식\; 2)$$

 

$f=1$을 넣었고, 적분식안에는 $y(t)$와 $e^{-2\pi t}$ 사이에는 내적 기호(dot)를 의도적으로 넣어 구분이 편하게 했다. 

 

이 식에서 복소지수로 표현된 부분을 삼각함수로 바꿔서 표현하겠다. 복소지수 표현이 간단하긴 하지만, 실제 어떤 값일까 하는 감을 잡기 위해서는 사인 함수로 표현하는 것이 좋다.

 

$$ Y(1) = \int _{-\infty} ^{\infty} {y(t) \cdot (\cos {2\pi t} - \sin {2\pi t})dt} \quad (식\; 2-1)$$

 

여기서 복소지수식을 삼각함수 식으로 바꾸는 것은 오일러 공식을 이용했다. ( 이 부분을 모르겠다면 04-3. 매클로린 급수, 오일러 공식 참조 )

 

$$ e^{i\theta} = \cos \theta + i\sin \theta$$

$$ e^{-i\theta} = \cos \theta - i\sin \theta$$

$$ e^{-i2\pi t} = \cos {2\pi t} - i\sin{2\pi t}$$

 

(식 2)를 계산하기 위해서는,

• 시간 $t$의 범위를 적절히 정하고, (변환식에서는 적분의 범위가 무한대이지만, 실제 무한대에 대해서 계산할 수 없다. 해서 적절한 시간 범위를 정해서 구해야 되고, 이 시간 범위를 무한대에 가깝게 크게 할수록 더 정확한 계산이 될 뿐이다.)
• 그 시간 범위에 대해서 적분식을 계산하면 될 것이다.

실제 계산을 하는 것은 다음 챕터에서 해볼것이고, 여기서는 그 의미를 파악하는 것이 그 목적이기에, 적분 안의 두 벡터의 곱에 대해 관심을 둬보다.

 

적분식 안에 보면 원래 시간에 대한 신호식인 $y(t)$가 있고, 이것에 대해 주파수가 $1$인 파형을 내적했다.

 

여기서 '내적'의 의미를 생각해보면, 벡터 연산에 있어서 두 벡터 $\vec A$와 $\vec B$의 내적은 "벡터 A의 벡터 B로의 사영(그림자)에 벡터 B의 크기를 곱한 값"이다. 

 

(식 2)에서 $\vec A=y(t)$이고, $\vec B=$(주파수 1일 때의 파형)이다. 그리고 주파수 1일 때의 파형에 대한 크기는 1이다. (복소평면에서 원의 반지름이 1이라는 것. $e^{i\theta}$는 반지름이 $1$이고 $3e^{i\theta}$의 반지름은 3)

 

그렇다면 (식 2)에서의 두 값의 내적이라는 것은 "원래 신호의 주파수 1인 파형으로의 그림자 크기"라고 할 수 있다. (벡터의 내적을 하게 되면 그 방향 성분은 사라지고 크기만 남는다.)

시간에 대한 파형을 주파수 1인 파형으로 정사영시킨 크기라는 말이다.

 

주파수 2에 대한 값인 $Y(2)$는 "원래 신호의 주파수 2인 파형으로의 그림자 크기"이고, $G(Y)$은 ....

 

정리하면, 푸리에 변환이라는 것은 "어떤 신호의 각각의 주파수로의 그림자 크기"를 구하는 변환식인 것이다.

 

---

잠시 벡터의 표현에 대해서 생각해 보자.

 

 

3차원 좌표에서 어떤 점 $P$가 있다고 하자.  이 $P$를 나타내려면 각 축의 벡터 성분 $\vec x$, $\vec y$, $\vec z$를 합하면 된다.  

 

$P$에 대해 나타낼 때 $X$와 $Y$의 성분만으로 표현하면 어떻게 될까? 

 

$$ \vec P = \vec x + \vec y $$

 

$Z$성분이 빠져서 완벽하지 않다. 그렇지만 어느 정도 $P$의 특성을 반영하기는 한다. $X$와 $Y$에 대한 특성은 나타냈으니.

 

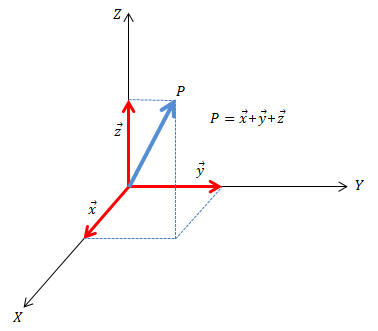
두 개 차원 혹은 한 개 차원으로 설명해도 그 나름대로 $P$에 대한 설명을 하는 것이다. 3가지 차원 성분 모두로 표현해야 완벽하겠지만.

 

---

다시 푸리에 변환식으로 돌아가자.

 

원래의 시간에 대한 파형을 위 벡터 설명에서의 점 $P$라고 생각해보자. 그리고, 각 주파수별로 하나의 축을 담당한다고 생각해 보자.

 

그렇다면 시간에 대한 파형은, 각 주파수 축으로의 성분들의 합으로 표현할 수 있다. 각 축에 대한 성분 크기는 원래의 파형과 각 축과의 내적을 하면 된다. 

 

원래의 파형을 완벽하게 설명하기 위해서는 무한대의 주파수 축을 이용해서 설명하면 된다. 그러나, 무한대의 주파수에 대해 계산한다는 것은 불가능하고, 어느 정도 범위와 레졸루션(주파수와 주파수 간격)을 정해서 그 해당 주파수 만으로 표현해도, 어느 정도는 그 파형을 설명할 수 있을 것이다.

 

이것이 푸리에 변환식의 의미이다. 신호를, 그 신호를 이루는 주파수 성분의 그림자로 표현하는 것이다.

 

푸리에 역변환도 위에서 설명한 논리와 똑 같이 생각할 수 있기에, 따로 설명하지 않겠다.

 

-끝-

 

이전글: 05. 푸리에 변환, 푸리에 역변환 (Fourier Transform, Inverse Fourier Transform)

다음글: 05-2. 한 신호를 정해서 손으로 푸리에 변환 해보기

다음다음글: 06. 이산 푸리에 변환 (DFT, Discrete Fourier Transform) --- 작성 중