앞 장에서 복잡한 신호를 여러 사인파의 합으로 나타내는 푸리에 급수를 알아봤다.
$ y(t) = a_0 + \sum _{n=1}^{\infty}{a_n \cos 2\pi nft + b_n \sin 2\pi nft} $ [식 1]
$ y(t) = a_0 + \sum _{n=1}^{\infty}{a_n \cos n\omega t + b_n \sin n \omega t}$ [식 2]
$ y(t) = a_0 + \sum _{n=1}^{\infty}{a_n \cos \frac {2\pi n}{T}t + b_n \sin \frac {2\pi n}{T}t} $ [식 3]
여기서 [식 2]를 주로 사용하겠다.
단위 시간에 얼마나 각이 빨리 변하는 지를 나타내는 각속도를 이용한 표현이다. $\omega$는 각속도를 의미하고 $\omega = 2\pi f$이기에 주파수에 $2\pi$를 곱한 값이다.
각속도를 이용한 표현을 주로 사용하는 이유는 식이 간단해지기 때문이다. 주파수를 이용할 때의 $2\pi$도 없고, 주기($T$)에 의한 표현으로 [식 3]에서는 분수를 썼어야 했는데, 각속도를 이용하면 분수표현도 사라져서, 식이 간단하게 된다.
| [식 2]를 주로 사용하겠다는 것이지 [식 1]과 [식 2]를 사용하지 않겠다는 것이 아니다. 세 식 모두 익숙하게 변형시킬 수 있어야 한다. |
이 식에서 $a_n$과 $b_n$을 '푸리에 계수'라 한다 했고, 이 계수가 있어야 이 식이 의미 있는 값이 된다.
이번 장에서 이 계수를 구해볼 것이다.
아래는 임의의 복잡한 파형이고, 이를 푸리에 급수를 이루는 각 요소별로 분해해본 그림이다. (사실은 단순한 파형들을 생성하고, 그 파형들을 합쳐서 복잡한 파형을 만들었다.)

위 그림을 그리는 파이썬 코드는 여기.
[그림 1]에서 제일 위에 있는 복잡한 신호는 푸리에 급수로 $y(t) = a_0 + \sum _{n=0}^{\infty}{a_n \cos n\omega t + b_n \sin n\omega t}$로 표현된다.
이 식의 각 요소인 $a_0, y(t)=a_1\cos\omega t, ...$를 그 밑에 그림으로 나타냈다.
(그림에는 $n=3$ 까지의 파형만을 그렸는데, 파이썬 코드로 실제 파형을 만들 때는 13개의 사인파를 이용했다.)
이 그림을 참조하면서 각 계수 값을 구하는 것을 설명하겠다.
1. $a_0$를 구하자.
먼저 $a_0$을 어떻게 구할지 생각해 보자.
$a_0$를 구한다는 것의 의미는, 그림의 제일 위에 있는 복잡한 신호가 있을 때(이러한 신호에 대한 정보가 우리에게 주어진 상태라고 생각하자), 이 복잡한 신호가 푸리에 급수 형태를 띨 텐데 그 계수 중에서 $a_0$값이 어떻게 될지 구해야 한다는 것이다. 즉, 복잡한 신호정보만 있는데, 거기에서 $a_0$값을 구하는 것이다.
어떻게 구할까?
힌트는 신호의 '적분'에 있다. 어떤 신호 혹은 그래프에 대해 '적분'한다는 의미는 그 그래프에 의해 만들어지는 면적을 구하는 것과 같다. (고등학교 수학에 나오는 개념이다.)
[그림 1]에서, 제일 위에 있는 신호를 구성하는 것이, 그 아래에 있는 그림들 전부이다. 따라서, 제일 위에 있는 신호에 대해 적분한 값과, 그 밑에 있는 나머지 파형들을 모두 적분한 값과는 같을 것이다.
하나씩 그 적분 값(=면적 값)이 어떻게 될지 살펴보자.
먼저, 제일 위에 있는 복잡한 신호에 대한 적분이다. 이것은, 실제 신호가 주어지면(시간에 대한 값으로), 신호에 의한 면적을 구하면 된다. (가로 축인 시간축을 잘게 쪼개면서 그 위치에서 그래프까지의 좁은 사각형들을 그려나가면서 면적을 구한다. 이러한 것을 정적분이라 하고, 컴퓨터 프로그램을 이용하면 가능하고, 지금은 정적분을 하는 것이 메인이 아니기에, 그냥 시간에 대한 그래프로 신호가 주어지면, 구할 수 있다고 생각하자)
신호에 대한 면적을 구하는 것은 적분을 하는 것이고, 이를 수식으로 표현하면 다음과 같다.
$$\int _{0}^{\infty}{f(t)dt}$$
신호 $f(t)$에 대해서 $t=0$에서 신호의 끝까지($t=\infty$) 면적을 구한다는 의미이다.
근데, 신호 전체에 대한 면적을 구해야만 할까? 무한대까지의 신호의 면적을 구하면 값이 무한대로 나와서 의미가 없을 것이다.
우리가 푸리에 급수에 대해 정의할 때 '주기 신호에 대해서'라고 단서를 달았다. 그렇다, 이 신호는 주기 T를 가지고 있고, 주기 신호는 $f(t) = f(t+T)$의 특성을 가지고 있다. 즉, 주기 T마다 같은 값을 가진다. 따라서, $t=0$에서 $t=T$까지의 한 개 주기만을 생각해도 되겠다.
즉, 복잡한 신호에서도 0~T까지 만을 고려하고, 복잡한 신호를 구성하리라고 예상되는 단순한 파형들에 대해서도 t=0~T까지 만을 고려하면 되겠다는 것이다.
그림에서 t=0~T까지 만을 빨간 박스로 칠해보자.
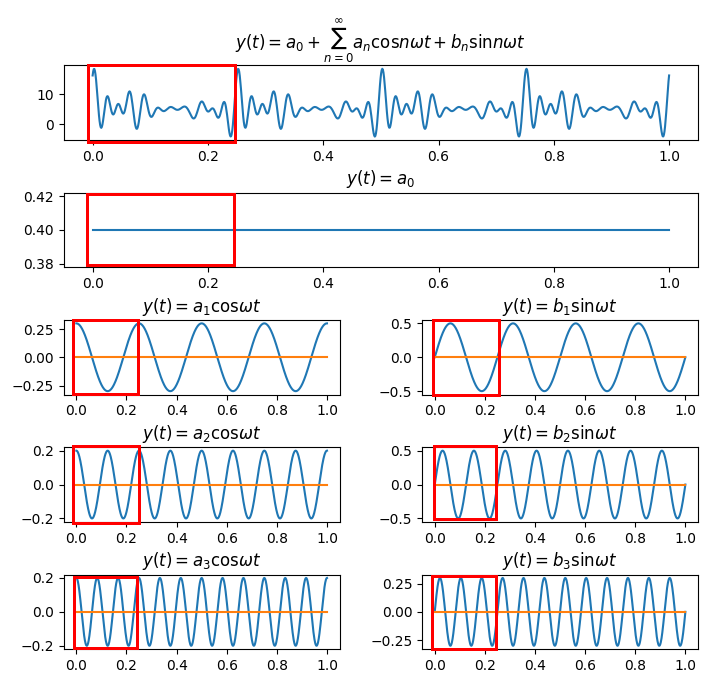
그림에서 빨간 박스로 그린 부분이 $t=0$에서 $t=T$까지의 부분이다. (실제 파이썬 코드로 파형을 생성할 때, 가장 낮은 주파수를 4로 했다. 즉, 1초에 4개의 파형이 반복되도록 했다. 따라서, 주기는 $\frac {1}{4} = 0.25$가 된다. 따라서, 위 그림에서 박스의 범위가 0~0.25초로 되는 것이다. )
| 편의상 0~T까지를 잡은 것이고, T~2T까지의 구간을 잡아도 상관없다. 한 개 주기이기만 하면 된다. |
이제 다시 신호 $y(t)$에 대해 0~T까지의 면적을 표현해 보면,
$$ \int _{0}^{T}{f(t)dt}$$
그림에서 두 번째 신호의 $y(t)=a_0$의 그래프에 대한 t=0~T까지의 면적을 생각해보자.
그래프가 $y=a_0$인 직선이기에 t=0~T까지의 면적은 $a_0 \times T$가 된다. 아래 그림을 보면 쉽게 이해될 것이다.

이 식에서 T는 알고 있다. (주어진 복잡한 신호의 T와 같고, 이 값은 우리가 이미 알고 있다. 즉, 복잡한 신호로부터 알아낼 수 있는 값이다.) 그렇다면, '면적'만을 어떤 다른 방법으로 우리가 알아낼 수 있다면, 계수 $a_0$값을 알아낼 수 있을 것이다.
이 면적을 어떻게 알아내는 가는 아래의 사인 함수, 코사인 함수에 의한 사인파들의 면적이 어떻게 되는지 알아보고 난 후 생각해보자.
[그림 2]에서 위에서 3번째부터 있는 코사인 곡선과 사인 곡선의 면적을 구해보자,
그래프를 자세히 보면, 모든 면적은 0(zero)이다.
사인 함수이건 코싸인 함수건 한 주기 동안의 적분 값(=면적)은 0이다. 위쪽 플러스(+) 영역과 아래쪽 마이너스(-) 영역의 크기가 같기에 서로 상쇄되는 것이다.
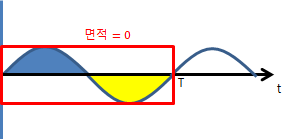
즉, 아래 그림과 같이, $y(t)=a_1\sin \omega t, y(t)=b_1\cos \omega t, y(t)=a_2\sin \omega t$ 등 모든 사인, 코사인 함수에 의한 파형들의 t=0~T까지의 면적이 0(zero)이다.
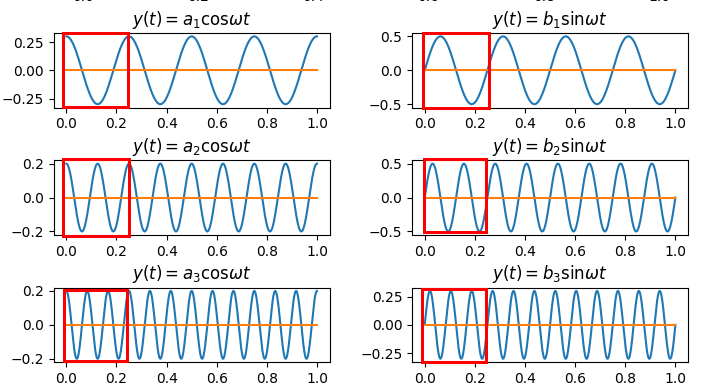
이제 전체 수식을 생각해보자.
복잡한 신호에 대한 적분 값은 $y(t)=a_0$인 그래프와 그 아래쪽에 있는 사인과 코사인 그래프의 면적을 전부 합한 것과 같기에 아래와 같은 수식이 된다.
$$ \int _{0}^{T}{f(t)dt} = T \times a_0 + 0 + 0 + ... $$
따라서, $a_0$를 다음과 같이 표현할 수 있겠다.
| $$ a_0 = \frac {1}{T} \int _{0}^{T}{f(t)dt}$$ |
주기 $T$는 알고 있는 거고, 신호 $f(t)$에 대한 적분 값은 계산할 수 있는 것이기에, 위 식으로 $a_0$를 알아낼 수 있겠다.
2. $a_1$을 구하자
$a_0$는 푸리에 급수 식 전체에 대해 적분을 취했는데, 우측 변에 있는 식들 중 코사인과 사인 함수로 되어 있는 부분의 면적이 0이 되고 $a_0$를 계수로 한 식만 남아서, $a_0$를 구하는 식을 얻을 수 있었다.
이제 코사인 함수의 계수인 $a_1, a_2,...$를 구하는 방법을 생각해 보자. 먼저 $a_1$에 대해서만 구해보자.
$a_0$를 구할 때와 마찬가지로 면적을 가지고 구해볼 것이다.
식을 다시 적어보자.
$ y(t) = a_0 + \sum _{n=1}^{\infty}{a_n \cos n\omega t + b_n \sin n \omega t} $ [식 4]
어떤 값을 더하거나 곱하거나 한 후 양변을 적분을 했을 때 $a_1$이 포함된 식만 남으면 되겠다.
방법은 양변에 $\cos \omega t$를 곱한 후 적분하면 된다.
진짜 그렇게 되는지 [식 4]의 양변에 $\cos \omega t$를 곱해보겠다.
$ y(t) \times \cos \omega t = a_0 \times \cos \omega t + $
$ a_1 \cos \omega t \times \cos \omega t + $
$ b_1 \sin \omega t \times \cos \omega t + $
$ a_2 \cos \omega 2t \times \cos \omega t + $
$ b_2 \sin \omega 2t \times \cos \omega t + $
$ a_3 \cos \omega 3t \times \cos \omega t + $
$ b_3 \sin \omega 3t \times \cos \omega t + ...$
식의 오른편 항목들에 대해서 적분을 했을 때 그 값이 어떻게 되는지 하나씩 알아보자.
1) $a_0 \times \cos \omega t $
코싸인 함수에 상수를 곱한 형태이다. 이것을 하나의 주기에 대해 적분하면 0이 된다.
이유는, 아래와 같이 코사인 함수에 상수를 곱해도 그 형태는 똑같고 진폭만 커지는 것이기에, $y=0$인 축을 기준으로 위쪽의 양의 면적(+)과 아래쪽의 음의 면적(-)의 크기가 같아서, 서로 상쇄되어 0이 된다.
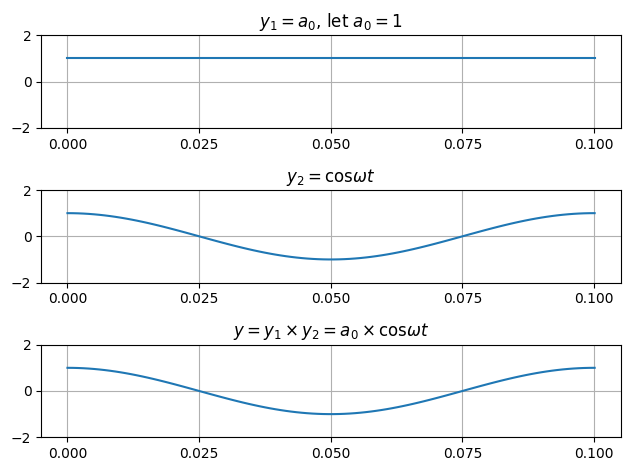
| 사인 함수와 코사인 함수에 대해서, 주기의 배수배 동안의 면적은 항상 0이다. 그리고, 상수배를 해도 면적은 0이다. 상수를 곱하는 것은 진폭만 커지기 때문에, 양수 방향의 면적과 음수 방향의 면적이 같은 것은 변함 없다. |
2) $a_1 \cos \omega t \times \cos \omega t$
같은 값이 $\omega t$를 가지는 $\cos$ 끼리의 곱이다.
그래프를 그려보면,
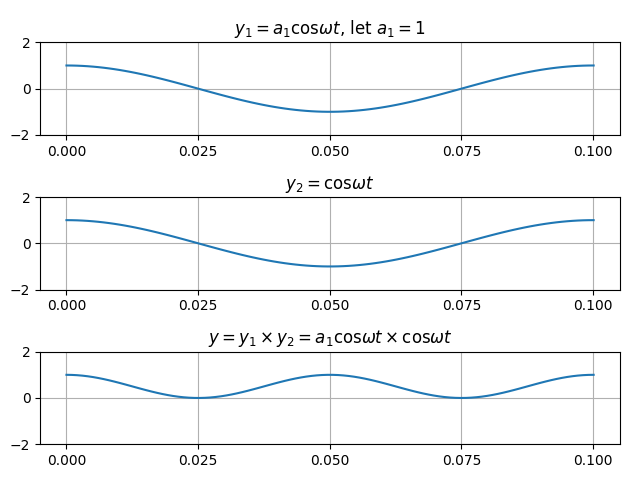
제일 아래쪽에 있는 것이 $a_1 \cos \omega t \times \cos \omega t$의 그래프인데, 면적의 합이 0이 아닌 것만은 확실하다. 모두 양수 방향의 면적이 있기 때문이다.
그래프를 좀 더 확대해서 자세히 알아보자.
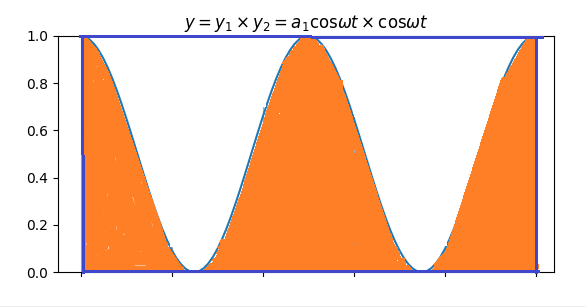
주황색을 칠해진 부분이 해당 면적이다.
위 그래프에서 $T=0.1$이고 $a_1=1$이다. 칠해진 부분의 면적은 얼마일까?
답은 0.05이다. 직사각형의 절반 면적인 $0.1 \times 1$의 절반 값이다.
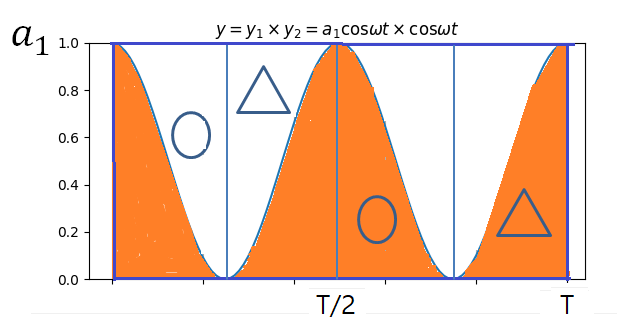
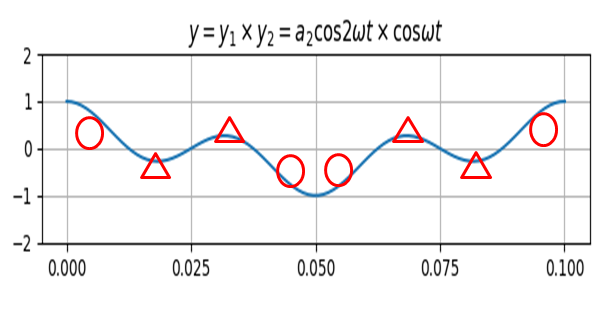
아래 그림에서 보듯이, 왼쪽 편에 있는 빈 공간에서의 동그라미와 세모 부분이, 오른편 사각형에 있는 빗금 친 영역의 동그라미와 세모 영영과 똑같기 때문에, 색칠된 영역의 크기는 직사각형의 절반 면적과 같다. 즉, $a_1 \times \frac {T}{2}$와 같다.
$$ \int _{0}^{T}{(a_1 \cos \omega t \times \cos \omega t)}dt=\frac {a_1 T}{2}$$
실제 적분 계산으로도 면적을 계산할 수 있다.
$\int _{ 0 }^{ T }{ (a_{ 1 } \cos\omega t\cos\omega t)dt } =\frac { a_{ 1 } }{ 2 } \int _{ 0 }^{ T }{ (\cos(\omega t+\omega t)+\cos(\omega t-\omega t))dt }$
$=\frac{a_{1}}{2} \int _{0}^{T}{(\cos 2\omega t + 1)dt}=\frac {a_{1}}{2}\int_ {0}^{T}{\cos2 \omega tdt}+\frac{a_{1}}{2}\int_ {0}^{T}{1dt}$
$ = 0 + \frac {a_1}{2} \biggl[ t \biggl]_0^T = \frac {a_1 T}{2} $
| 위 계산에서 삼각함수의 곱셈 공식이 사용되었다. $\cos A \cos B = \frac {1}{2} (\cos (A+B) + \cos (A-B))$ 따라서, $a_1 \cos \omega t \cos \omega t = \frac {a_1}{2} (\cos (\omega t + \omega t) + \cos (\omega t - \omega t))$ 가 된 것이다. 그리고 계산 중에 삼각함수의 한 주기 동안의 면적은 0이 된다는 것이 이용되었다. $\int _{0}^{T}{\cos \omega tdt} = 0$ |
3) $ b_1 \sin \omega t \times \cos \omega t$
이제 $b_1 \sin \omega t$와 $\cos \omega t$와의 곱을 알아보겠다.
그래프를 그려보면, 면적이 0이 될 거 같음을 알 수 있다.
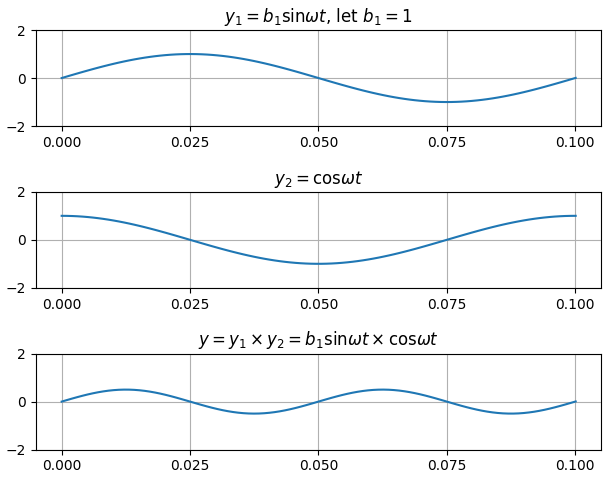
수식으로도 풀어보자.
먼저 삼각함수의 곱셈 공식 $\sin A \cos B = \frac {1}{2} (\sin (A+B) + \sin (A-B))$를 이용하면 $b_1 \sin \omega t \cos \omega t = \frac {b1}{2} (\sin (\omega t+ \omega t) + \sin (\omega t - \omega t)) = \frac {b_1}{2} \sin 2 \omega t$ 가 된다. 이것에 대해 0~T까지의 적분을 해보면,
$\frac {b_1}{2} \int _{0}^{T}{\sin 2\omega t}dt =0 $
수식으로도 역시 0이 됨을 알 수 있다.
4) $a_2 \cos 2\omega t \times \cos \omega t$
이제 같은 $\cos$인데, $2\omega t$와 $\omega t$로 주파수가 다른 두 파형의 곱에 대해 알아보자.
그래프를 그려보면, 역시 면적의 합이 0이 될 거 같다.
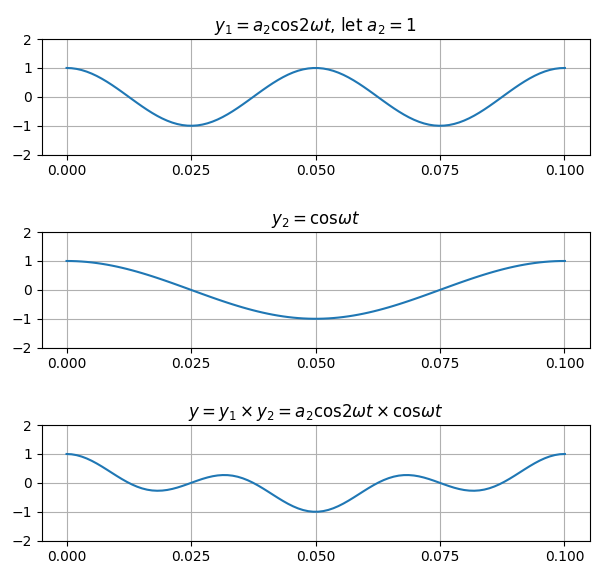
곱해진 파형을 좀 더 확대해 보면, 양의 부분 면적과 음의 부분 면적이 같음을 알 수 있다.
수식으로 면적의 합을 구해보자.
삼각함수의 곱셈 공식 $\cos A \cos B = \frac {1}{2}(\cos (A+B) + \cos (A-B))$에 의해 $a_2 \cos 2\omega t \cos \omega t = \frac {a_2}{2}( \cos (2 \omega t + \omega t) + \cos (2\omega t - \omega t) ) = \frac {a_2}{2} (\cos 3\omega t + \cos \omega t)$가 된다. 이에 대해 0~T까지의 적분을 하면,
$\int _{0}^{T}{\frac {a_2}{2} (\cos 3\omega t + \cos \omega t)} = 0$
왜냐하면, 한 주기 동안의 $\cos$ 함수에 대한 적분 값은 0이기에 $\int _{0}{T}{\cos 3\omega tdt}=0$이고 또한 $\int _{0}^{T}{\cos \omega tdt}=0$이기 때문.
5)$b_2 \sin 2\omega t \times \cos \omega t$
주파수가 다른 $\sin$과 $\cos$과의 곱이다.
역시 그래프를 그려보면, 면적의 합이 0이 됨을 알 수 있다.
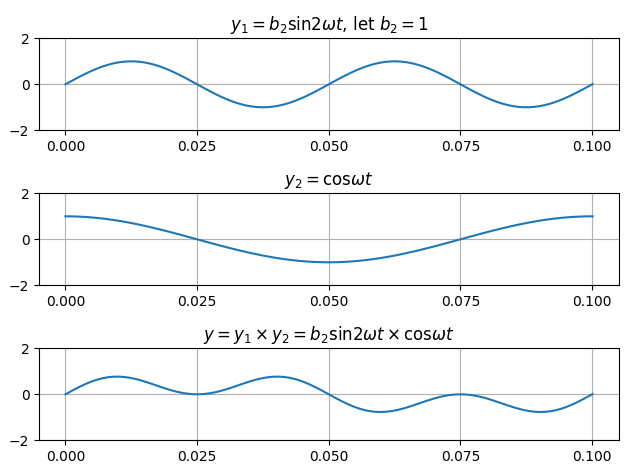
수식으로 계산해봐도 역시 0이다.
삼각함수 곱셈 공식인 $\sin A \cos B = \frac {1}{2}(\sin (A+B) + \sin (A-B))$를 이용하면 $b_2 \sin 2\omega t \cos \omega t = \frac {b_2}{2} (\sin 3\omega t + \sin \omega t)$이다.
이에 대해 적분을 해보면, 값이 0이 된다.
$\int _{0}^{T}{\frac {b_2}{2} (\sin 3\omega t + \sin \omega t)}dt = 0$
왜냐하면 $\int _{0}^{T}{\sin 3\omega t}dt = 0$이고 또한 $\int _{0}{T}{\sin \omega t}dt =0$ 이기 때문이다.
이제 정리를 해보면,
$ \int _{0}^{T}{y(t) \times \cos \omega t}dt = \int _{0}^{T}{ [ a_0 \times \cos \omega t + } $
$ a_1 \cos \omega t \times \cos \omega t + $
$ b_1 \sin \omega t \times \cos \omega t + $
$ a_2 \cos \omega 2t \times \cos \omega t + $
$ b_2 \sin \omega 2t \times \cos \omega t + $
$ a_3 \cos \omega 3t \times \cos \omega t + $
$ b_3 \sin \omega 3t \times \cos \omega t + ...] dt$
위 식에서 각 적분 값은,

즉,
$$ \int _{0}^{T}{y(t) \times \cos \omega t}dt = \frac {T}{2} a_1$$
$$ \therefore a_1 = \frac {2}{T} \int _{0}^{T}{y(t) \cos \omega t}dt$$
오른 편의 적분 값을 알 수 있기에 결국 $a_1$값을 구할 수 있겠다.
$a_1$에 이어 $a_2$를 구하기 전에, $a_1$ 값을 구할 때, 적분 값이 0이 되는 사인 및 코사인 함수의 곱끼리의 관계를 정리해보자.
모두 하나의 주기에 대한 적분 값이었고, 이에 대한 경우의 수를 나눠서 어떤 값이 나오는지 정리해본다.

정리된 사항을 더 간단히 얘기하면, 한 주기에 대한 면적합은(=적분 값은), 같은 주파수에 대한 $\sin \times \sin $과 $\cos \times \cos$을 제외하고는, 모두 값이 0이 된다.
위 표에서 4번과 5번의 사인 코사인 곱 조합에 대해 적분 값이 0이 되는 이유를 수식 관점에서 살펴보자.
삼각함수의 곱셈 공식은 아래와 같다.
$ \sin A \cos B = \frac {1}{2} (\sin (A+B) + \sin (A-B))$ (1)
$ \cos A \sin B = \frac {1}{2} (\sin (A+B) - \sin (A-B))$ (2)
$ \cos A \cos B = \frac {1}{2} (\cos (A+B) + \cos (A-B))$ (3)
$ \sin A \sin B = -\frac {1}{2} (\cos (A+B) + \cos (A-B))$ (4)
표의 4번 경우를 보면, 식 (3)과 식(4) 번에서 $A \neq B$의 경우이다. 따라서 식에서 $A+B$ 및 $A-B$의 값이 0이 아닌 값을 가지게 되고, 이것을 한 주기 동안 적분하게 되면 0이 될 것이다.
표의 5번의 경우는 식 (1)과 식 (2)에 해당하는데, $A=B$의 경우는 식의 앞 쪽은 $\sin (A+B) = \sin 2A$ 이기에 한 주기 동안의 적분 값은 0이고, 뒤 편에 있는 $\sin (A-B) = \sin 0 = 0$이 되어, 0에 대한 적분은 역시 0이기에, 전체 적분 값이 0이 된다.
$A \neq B$의 경우에는, 앞 쪽 부분도 뒤 쪽 부분도 모두 어떤 값을 가지고 있고, 이 경우 한 주기 동안의 적분 값이 0이기에 전체 적분 값은 0이 된다.
쉽게 생각하면, 한 주기 동안의 사인, 코사인 곱에 대한 적분 값이 0이 아닌 것은, $\cos A \cos A$ 혹은 $\sin A \sin A$의 경우 만인데, 그 이유는 식 (3)과 식 (4)에서 뒤 편의 $\cos (A-B) = \cos 0 = 1 $이 되어, 1에 대한 적분 값이 존재할 때만이다. 1에 대한 한 주기 동안의 적분 값은 $T$이고, 식 앞에 있는 $\frac {1}{2}$이 곱해져서 전체 적분 값은 $\frac {T}{2}$가 된다. (만약 진폭 값이 있는 경우는 $\frac {T}{2}$에 그 진폭 값이 곱해진 것이 전체 적분 값이 될 것이다. )
3. $a_2$를 구하자
지금까지 $a_0$과 $a_1$을 구해봤고, $a_1$을 구할 때는 $a_1$과 결합되어 있던 $\cos \omega t$를 푸리에 급수 식의 양변에 곱한 후 적분을 해서 구했다.
$a_2$를 구할 때도 푸리에 급수 식의 양변에 $a_2$와 결합되어 있는 $\cos 2\omega t$를 곱한 후 적분하면 될 것이다.
이유는, 위에서 사인, 코사인 곱에 대한 한 주기 동안의 적분에서 알아봤듯이, 같은 코사인 값에 대한 곱의 경우만 값이 남고 나머지 곱 조합의 경우는 모두 0이 되기 때문이다.
이 경우도 $\cos 2 \omega t $를 양 변에 곱하고 적분하면, 오른편에는 $a_2 \cos \omega t$에 대한 적분 값만 남게 될 것이다.
$ \int _{0}^{T}{y(t) \times \cos 2\omega t}dt = \int _{0}^{T}{ [ a_0 \times \cos 2\omega t + } $
$ a_1 \cos \omega t \times \cos 2\omega t + $
$ b_1 \sin \omega t \times \cos 2\omega t + $
$ a_2 \cos \omega 2t \times \cos 2\omega t + $
$ b_2 \sin \omega 2t \times \cos 2\omega t + $
$ a_3 \cos \omega 3t \times \cos 2\omega t + $
$ b_3 \sin \omega 3t \times \cos 2\omega t + ...] dt$

식을 정리해 보면,
$\int _{0}^{T}{y(t) \times \cos 2\omega t dt} = \frac {T}{2} a_2$
$\therefore a_2 = \frac {2}{T} \int _{0}^{T}{y(t) \cos 2\omega t dt}$
4. $a_n$에 대한 일반 식
$a_1$은 푸리에 급수식에서 $\cos \omega t$를 곱한 후 적분해서 $\frac {2}{T} \int _{0}^{T}{y(t) \cos \omega t dt}$, $a_2$는 $\cos 2 \omega t$를 곱한 후 적분에 의해 $\frac {2}{T} \int _{0}^{T}{y(t) \cos 2 \omega t dt}$가 되었다.
그렇다면 $a_3$는 $\cos 3 \omega t$를 곱해서 $\frac {2}{T} \int _{0}^{T}{y(t) \cos 3\omega t dt}$를 얻을 수 있을 것이고, 일반화하면 $a_n = \frac {2}{T} \int _{0}^{T}{y(t) n \omega t dt}$가 될 것임을 알 수 있다.
따라서 $a_0$와 $a_n, n=1,2,3,...$ 값을 정리하면,
$$ a_0 = \frac {1}{T} \int _{0}^{T}{y(t) dt}$$
$$ a_n = \frac {2}{T} \int _{0}^{T}{y(t) \cos n \omega t dt}$$
5. $b_n$ 구하기
$b_1$에 대해서도 $a_1$을 구할 때와 마찬가지로, $b_1$과 결합되어 있는 $\sin \omega t$를 푸리에 급수식에 곱한 후 적분해보면 $b_1$을 구할 수 있겠다.
$ \int _{0}^{T}{y(t) \times \sin \omega t}dt = \int _{0}^{T}{ [ a_0 \times \sin \omega t + } $
$ a_1 \cos \omega t \times \sin \omega t + $
$ b_1 \sin \omega t \times \sin \omega t + $
$ a_2 \cos \omega 2t \times \sin \omega t + $
$ b_2 \sin \omega 2t \times \sin \omega t + $
$ a_3 \cos \omega 3t \times \sin \omega t + $
$ b_3 \sin \omega 3t \times \sin \omega t + ...] dt$

따라서, $b_1 = \frac {2}{T} \int _{0}^{T}{y(t) \sin \omega t dt}$
마찬가지 방법으로 $b_2$를 구하기 위해 $\sin 2 \omega t$를 곱해서 구하면, $b_2 = \frac {2}{T} \int _{0}^{T}{y(t) \sin 2\omega t dt}$
$b_n$에 대해 일반화하면,
$$b_n = \frac {2}{T} \int _{0}^{T}{y(t) \sin n \omega t dt}$$
이제 푸리에 급수에 대한 계수를 구하는 식까지 알아냈다.
푸리에 급수는,
| $ y(t) = a_0 + \sum _{n=1}^{\infty}{a_n \cos n\omega t + b_n \sin n \omega t}$ |
푸리에 계수는,
| $ a_0 = \frac {1}{T} \int _{0}^{T}{y(t) dt}$ $ a_n = \frac {2}{T} \int _{0}^{T}{y(t) \cos n \omega t dt}$ $b_n = \frac {2}{T} \int _{0}^{T}{y(t) \sin n \omega t dt}$ |
복잡한 신호일지라도 주기성만 보인다면, 그 주기보다 짧은(정확하게는 그 주기의 정수배만큼 짧은) 사인파들의 선형 결합(임의의 계수를 곱하고 서로 더하는)으로 표현할 수 있다는 것이 푸리에 급수였고, 그 푸리에 급수에 사용되는 계수들은 원래의 복잡한 신호에 사인파 신호들을 적절히 곱하면서 적분을 하면 구할 수 있다는 것이, 이번 장에서 배운 내용이다.
더 쉽게 얘기하면, 복잡한 신호를 여러 개의 단순 신호로 쪼개서 표현할 수 있다는 것이다.
비유하자면, 어떤 맛있는 찌개가 나왔는데, 거기에 들어간 재료들과 그 양을 알 수 있는 식이 있다는 것이다. (수학적으로 적적할 비유는 아니지만, 푸리에 급수의 의미를 파악하는 데는 괜찮은 비유)
다음 장에서는 이 푸리에 급수의 표현을 복소 지수로($e^{i\theta}$) 표현하는 방법에 대해 알아볼 것이다.
굳이 복소지수로 표현하는 이유는, 복소지수로 표현했을 때라야만 의미 있는 상황들이 있기 때문이다.
-끝-
| 이전글: 02-3. 푸리에 급수: 사인파의 합을 통해 복잡한 파형 만들기 |
| 다음글: 04. 푸리에 급수의 복소지수 표현 |
| 다음다음글: 04-1. 복소 평면, 복소평면에서의 원 |
'푸리에 변환, 신호 > 푸리에 변환의 모든 것' 카테고리의 다른 글
| 04-1. 복소 평면, 복소평면에서의 원 (5) | 2020.10.11 |
|---|---|
| 04. 푸리에 급수의 복소지수 표현 (0) | 2020.10.11 |
| 02-2. 푸리에 급수: 사인파의 합을 통해 복잡한 파형 만들기 (4) | 2020.10.01 |
| 02-1. 푸리에 급수: 사인파의 표현 방법(사인함수, 각속도, 라디안) (10) | 2020.10.01 |
| 02. 푸리에 급수 : 주기신호, 삼각 함수(사인, 코사인 그래프) (3) | 2020.09.15 |



