04-1. 복소 평면, 복소평면에서의 원

복소평면에서의 원

복소평면에서의 원에 대한 미분을 알아볼 것이다.  뜬금없을 수도 있으나, 이 글의 끝까지 가보면 왜 이것에 대해 알아보는지 이유를 알 수 있을 것이다.  

 

이를 위해서 우리는, 복소평면이 무엇인지도 알아야겠고, 원이 어떻게 표현되는지도 알아야한다.

 

---

복소평면

복소평면은 실수와 허수를 모두 표현하기 위한 평면 공간이다. (복소평면을 '가우스 평면'이라고 한다.)

 

허수는 제곱했을 때 $-1$이 되는 수 $i$를 포함한 수이다. ($2i, 3i$ 등)

$$ i^2 = -1$$

$$ i = \sqrt {-1}$$

 

허수 $i$가 도입된 것은 $x^2 = -1$을 만족하는 수를 표현하기 위함이었다.  수학에서는 $i$라고 표현하고, 전기/전자 공학 쪽에서는 $j$라는 표기를 사용한다. 전류를 나타내는 $i$와의 혼돈을 피하기 위해서일 것이다. 이 글에서는 허수에 대한 표시로 $i$를 사용할 것이다. 그러나 가끔 $j$가 사용되는 곳도 있을 수 있다.

 

우리가 일반적으로 실수 $x$를 가로축으로, 실수 $y$를 세로축으로 표현하는 것은 그냥 실수 공간이다. 단지 가로 축의 1차원과 세로 축의 1차원을 이용해서 (x, y)의 2차원 공간을 표현할 뿐이다. 

 

이와 달리 복소평면은 가로축을 실수로, 세로축을 허수로 표현하는 공간이다. 

 

 

복소평면공간(혹은 복소 공간)에서 $3+4i$라고 하면, 중간에 있는 덧셈에 현혹되지 말고, 공간 내에서의 좌표 개념으로 $(3,4i)$의 '지점'을 떠올리는 것이 낫다.

 

덧셈(+)으로 표현한 것은 벡터(Vector)의 표현 방법이다. 두 벡터 $\vec a$와 $\vec b$가 있을 때, $\vec a + \vec b$는 서로 90도인 축으로 이루어지는 공간에서, 두 값에 의한 좌표를 의미한다.  

 

복소 평면과 실수 평면(그냥 실수 축 2개로 이루어진 2차원 실수공간)과 어떻게 다른 것일까? 복소 평면이 어차피 두 개의 좌표를 나타낸다면 그냥 2차원 실수 공간을 사용해도 되지 않을까? 답은 그렇지 않다 이다. 실수 2차원 공간에서는 허수 축 값에 대한 $i^2=-1$이 되는 특성이 없다.  따라서, 실수 2차원 좌표로는 원의 회전, 전기 신호에서의 위상차 등의 표현이 힘들다.  복소 평면을 이용하면, 그냥 실수 공간에 의해서는 표현할 수 없었던 신호 특성(회전 혹은 신호의 위상차 등)을 표현할 수 있다. 따라서, 그냥 정적인 좌표를 나타낼 때는 그냥 실수 좌표계를 사용하는 것이 편하고, 파형 신호 등 동적인 성질을 표현해야 할 때는 복소 평면을 사용해야 하는 것이다.

 

 

 

복소 표현에서 허수부는 의미 없는 수가 아니다. '허수'라는 단어를 사용해서 그런지, 종종 허수로 표현된 값이 '그냥 무시해도 되는 값'으로 인식하는 경우가 있는데, 그렇지 않다. 복소 평면에서 세로 축의 값을 나타내는 중요한 값이다. 단지 '실수'라는 단어에 대응되어 '허수'라는 단어가 존재하고, 복소 평면에서 세로 축을 허수로 나타내기로 약속 했기 때문에 허수로 나타내는 것 뿐이다.

 

---

복소평면에서의 원의 표현

복소평면에서 실수 축 값이 $a$이고 허수 축 값이 $bi$인 $C$라는 값은 $C=a+bi$로 표현된다.

 

그런데 여기서 $a$와 $b$를 고정된 값이 아니라 어떤 변수 $x$에 대한 함수로 두면 어떻게 될까?

 

$a$는 어떤 함수 $p(x)$에 의한 값이고, $b$는 또 다른 함수인 $q(x)$에 의한 값이라는 것이다.

 

$$ a = p(x), b=q(x)$$

$$ C = a+bi = p(x) + q(x)i$$

 

예를 들어 $a=x$이고 $b=1/x$라고 해보자. ($p(x)=x$이고 $q(x)=1/x$ )

 

$x$에 따라 $a, b$ 값이 바뀐다. 몇 개를 계산해 보면,

 

$x=0$인 경우는 존재하지 않는다. (이 경우 b의 값이 $1/0$으로 분모에 0이 들어가는, 존재하지 않는 수가 된다)

 

$a=x$이고, $b=1/x$이기에 $b=1/a$과 같다. 즉, $(x, y)$로 이루어진 실수 평면에서 $y = 1/x$의 그래프와 똑 같이 될 것이다.

 

실제로 엑셀에서 그래프를 그려보면 아래와 같이 된다.

 

 

---

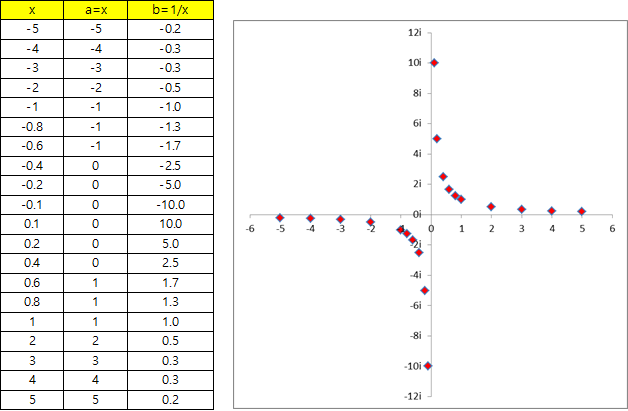
복소평면에서 $a, b$ 값에 따라 어떻게 위치를 찍는지 충분히 감이 잡혔을 것이다. 

 

그렇다면 이제, 이 복소평면에서 원을 그리는 식을 생각해내 보자. 즉, $a=p(x), b=q(x)$에서 $p(x)$와 $q(x)$를 어떻게 정하면 x의 변화에 따라 복소평면에서 원이 그려질까? 하는 문제이다.

 

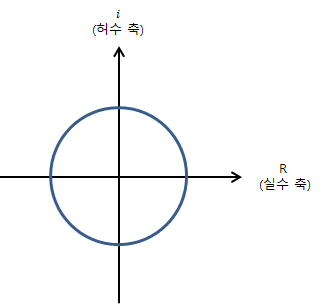
먼저, 반지름이 1인 원을 그리는 것으로 하고, 원을 그릴 때 실수 축 1인 지점에서 반시계 방향으로 원을 그린다고 생각해보자. 

 

 

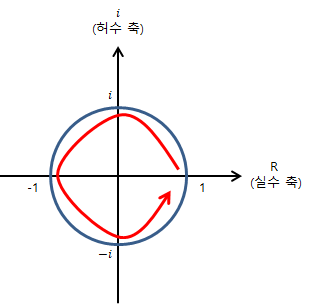
그럼 이때 $a$의 실수 축 값은 어떻게 변할까? 즉, 원을 그려나감에 따라 그 원의 한 지점에서 실수 축으로 수선을 내렸을 때의 지점이 어떻게 변하는가 하는 것이다.

 

답은 실수 값 1에서 -1까지의 왼쪽 편으로 갔다가, 1이 있는 방향으로 이동한다. 

 

복소평명에서 원이 그려짐에 따라 실수축 변화 값(출처:자작 https://github.com/rhaos68/fourier/blob/master/circle_on_complex_plane.py  CircleOnComplexPlane class)

 

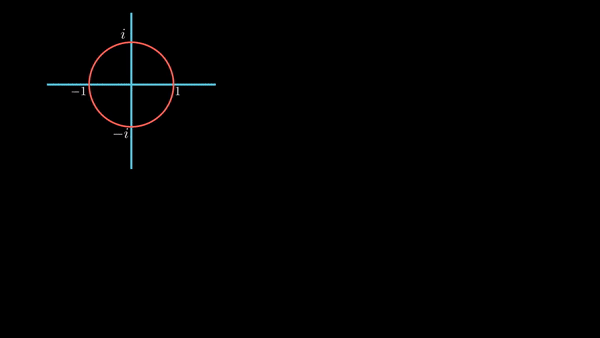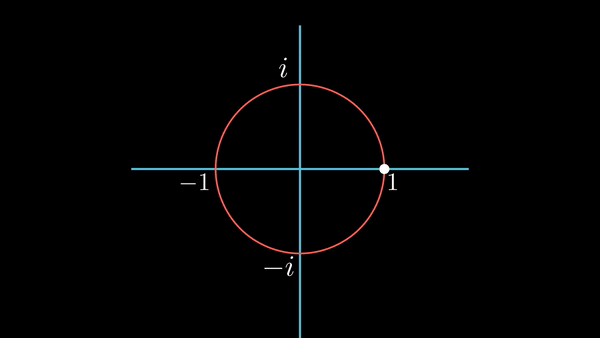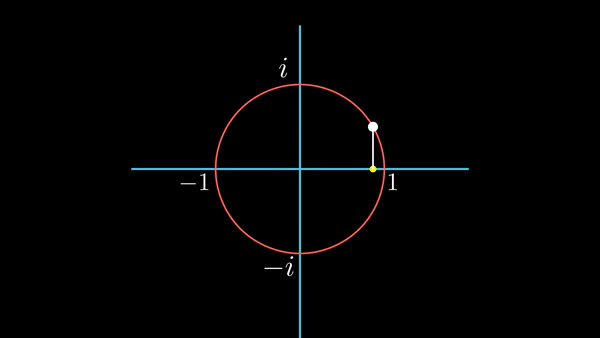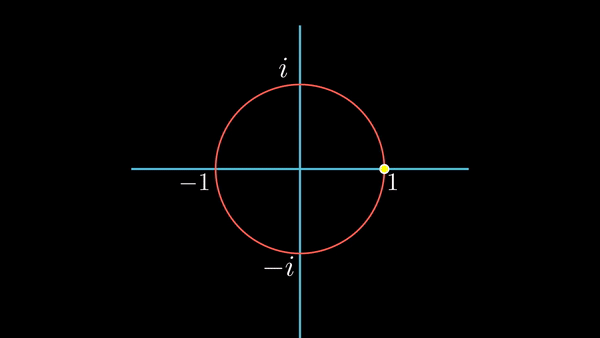
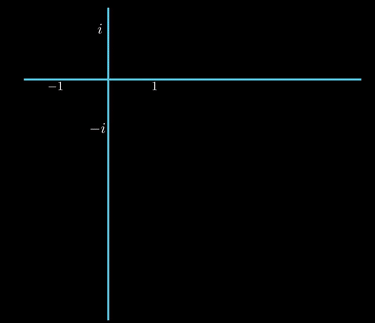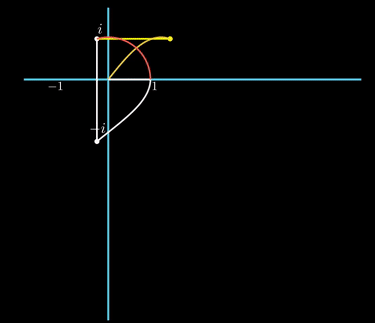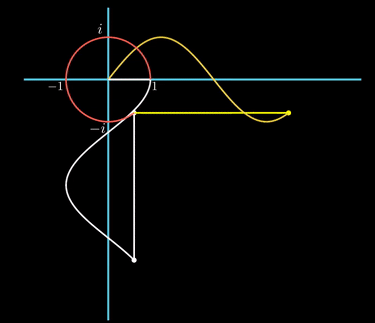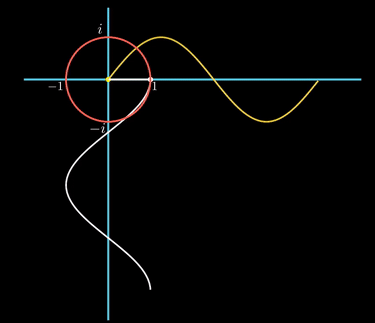
실수 축을 따라 좌/우로 이동하는 것을, 시간의 흐름에 따라 표현해보자. 즉, 아래 방향으로의 직선을 시간의 흐름으로 놓고, 원이 그려질 때의 실수 축의 값을 아래 방향으로 쉬프트 하는 것이다.

 

복소평명에서 원이 그려짐에 따라 실수축 변화 값은 코사인 그래프를 그림(출처:자작 https://github.com/rhaos68/fourier/blob/master/circle_on_complex_plane.py  CircleOnComplexPlane_COS class)

 

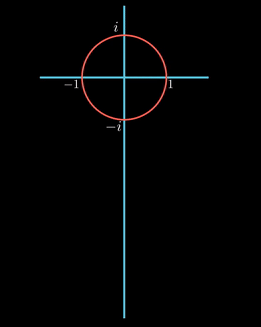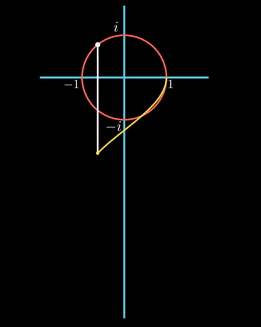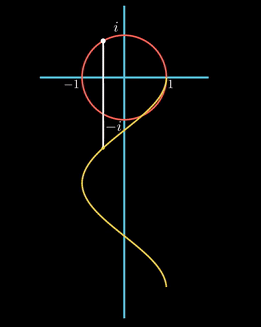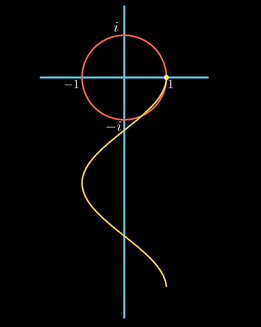
그려지는 곡선을 보면 진폭이 1이고, 출발점에서 값이 1이고, 원이 한 바퀴도는 시간을 한 주기로 가진다. 코사인 곡선이다.  즉, 실수 축의 값은 $a=\cos x$라고 할 수 있다. 

$$ a=\cos x$$

 

앞 쪽에서 이러한 원리로, 원으로부터 코사인 곡선을 만들어내는 것을 살펴봤었다. https://infograph.tistory.com/221

 

여기서 $x$는 시간일 수도 있고, 원을 그릴때 원점에서 원위의 점(펜으로 원을 그린다면 그 펜의 위치)으로의 선분에 대한 각도 일 수도 있다.  즉, 원을 그림에 따라 증가하게되는 모든 것이 $x$가 될 수 있고, 여기서는 주로 '각도'를 많이 이용할 것이다.

 

허수 축에 대해서도 똑같은 방법을 적용해 보자. 원이 그려질 때 허수 축의 값 $bi$가 어떻게 변하는지 생각해보는 것이다.

 

원을 그려가면서 원 위의 점에서 허수 축으로의 수선을 내려서 만나는 점을 따라가 보면 되는 것인데, 원이 그려짐에 따라 0에서 위 쪽으로 이동하다가 $i$에서 다시 아래쪽으로 내려가서 $-i$까지 가고, 거기서 다시 $0$까지 올라가게 된다. 

 

이렇게 그려지는 것을 애니메이션으로 표현해 봤다.

 

복소평명에서 원이 그려짐에 따라 허수축 변화 값(출처:자작 https://github.com/rhaos68/fourier/blob/master/circle_on_complex_plane.py  CircleOnComplexPlane_Imaginary class)

 

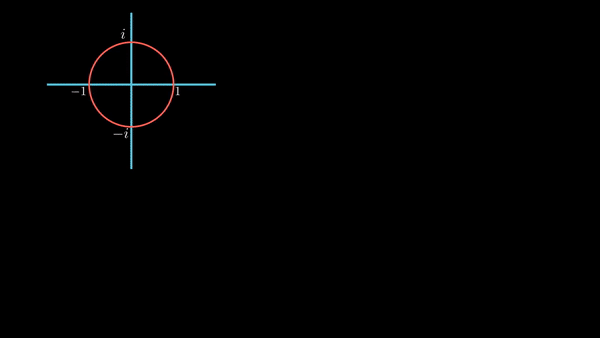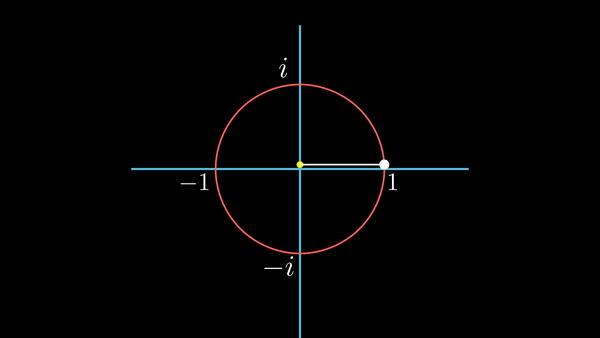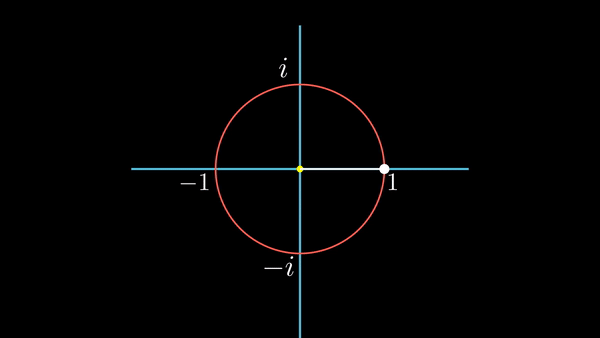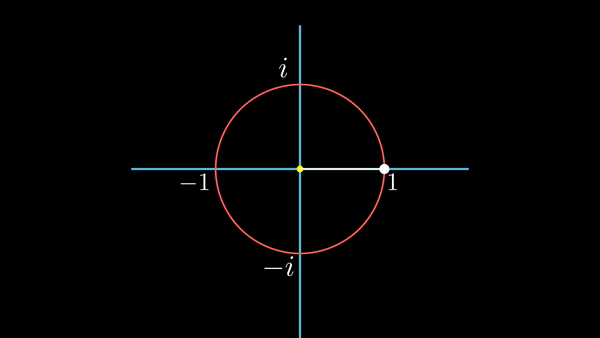
허수 축을 따라 위아래로 움직이는 것을 시간의 흐름에 따른 위치로 표현해본다. 시간이 흐름에 따라 가로축 오른편으로 이동하면서 허수 축의 점을 찍어 보는 것이다. 아래 그림을 보자.

 

복소평명에서 원이 그려짐에 따라 허수축 변화 값은 사인 그래프를 그림(출처:자작 https://github.com/rhaos68/fourier/blob/master/circle_on_complex_plane.py  CircleOnComplexPlane_SIN class)

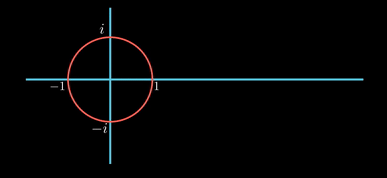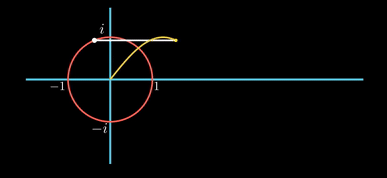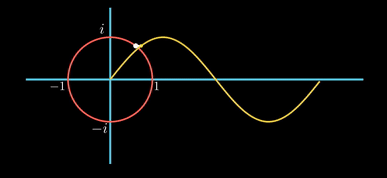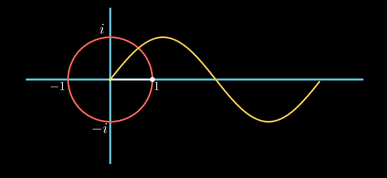
그려지는 곡선을 보면, 시작점에서의 값이 0이고, 진폭은 1이며, 원 한 바퀴 돌 때마다 한 주기를 가지는 곡선이다. 사인 곡선이다. 따라서, 허수 축 $b$의 움직임을 나타내는 함수는 $b=\sin x$라고 할 수 있다. 

$$ bi = \sin x \cdot i = i \sin x$$

 

$a$와 $b$에 대한 함수 식을 종합해보면, 복소평면에서 반지름 1인 원을 만드는 함수 식 $C(x)$는 $\cos x + i\sin x$가 된다.

 

$$ C(x) = \cos x + i \sin x$$

 

---

식을 유도하기 위해서 원을 그려나가며 실수 값의 변화식, 허수 값의 변화식을 알아봤는데, 반대로 얘기하면, 실수 축 값을 $\cos x$에 따라 바꾸고, 동시에 허수 축 값을 $\sin x$에 따라 변화시키면, 이에 의해 복소평면에 원이 그려진다라고 할 수 있다. 

 

코사인과 사인 함수에 의해 원이 생성됨(출처:자작 https://github.com/rhaos68/fourier/blob/master/circle_on_complex_plane.py  CircleOnComplexPlane_SINCOS class)

 

위 애니메이션은 시간축을 따라 진해되는 $\cos x$, $\sin x$를 기준으로 원을 그리는 모습을 보여주고 있는데, 여기서 시간축을 없애고 그냥 실수 축에서의 $\cos x$, 허수 축에서의 $\sin x$값의 이동을 가지고 그려보면 아래와 같이 된다. 실수 축 값도 그렇고 허수 축 값도 마찬가지로 [-1, 1] 사이에서만 값이 변화된다.

 

코사인과 사인 함수에 의해 원이 생성됨(출처:자작 https://github.com/rhaos68/fourier/blob/master/circle_on_complex_plane.py  CircleOnComplexPlane_SINCOS2 class)

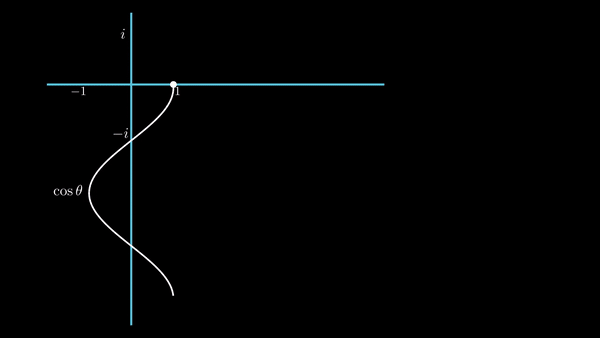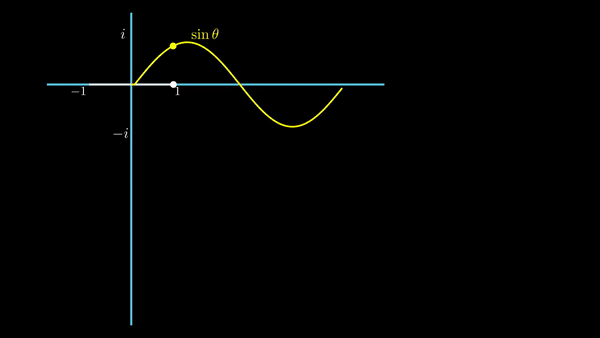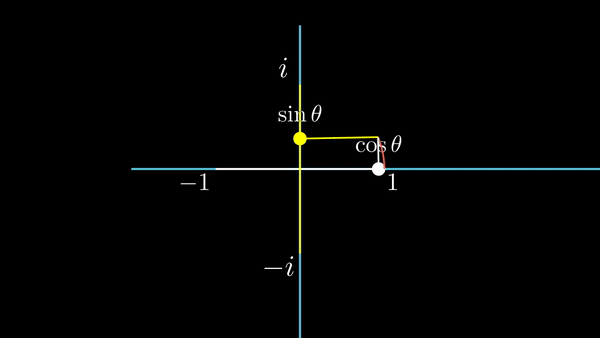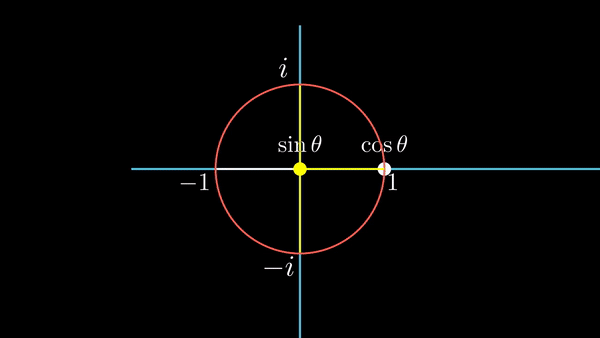
복소평면에서의 원을 만드는 식이 코사인과 사인함수의 합으로 표현되었다. 이것은 마치 앞 쪽의 장에서 살펴봤던, 사인파를 $A\cos \theta + B \sin \theta$로 나타냈던 것과 유사하다. 사실 그런 목적으로 복소평면에서 원을 만들어보자고 한 것이다.  이런 유사성 및 의미는, 이 장의 최종 목적지인 푸리에 급수의 복소지수 표현을 설명하면서 그 의미가 파악될 것이다.

 

 

-끝-

 

 

이전글: 04. 푸리에 급수의 복소지수 표현

다음글: 04-2. 복소 지수, 자연 상수 e

다음다음글: 04-3. 매클로린 급수, 오일러 공식