앞 챕터에서 주기적인 신호를 표현하기 위한 가장 단순한 함수로 '사인 함수'를 후보로 해서 알아봤다.
사실 지금까지의 신호 이론은 '모든 신호는 단순한 신호의 조합으로 나타낼 수 있고, 이 단순한 신호는 사인파로 나타낼 수 있다'에서 출발한다. 그리고 실제로 모든 신호를 이러한 이론적 근거로 해서, 단순한 신호의 조합으로 나타낼 수 있다.

여기서 사인파는 사인 함수인 sine 혹은 cosine으로 나타낼 수 있는 파형으로, 정현파(正弦波)라 하고 영어로는 Sinusolidal Signal이라고 한다.
| 정현파라는 것은 '활'의 모양을 빗대어 부른 말로 사인파(sine wave)가 이에 해당한다. 코사인 함수로 이루어진 파형을 '여현파'라고도 하는데, 어차피 사인파를 평행이동 시키면 코사인파가 되기에, 구분해서 부르는게 큰 의미가 없을 것이다. 해서, 영어로는 Sinusolidal Signal 이라고 한 가지 용어만 쓰이고 있고, 이 Signusolidal Signal을 sine 혹은 cosine 함수로 나타낼 수 있는 것이다. 여기서는 그냥 '사인파'라고 사용하기로 하겠다. '정현파'라는 말은 일본식 표현을 그대로 쓴 느낌이어서 별로 쓰고 싶지 않다. |
사인파의 생성
사인파는 sin 혹은 cos 함수로 나타낼 수 있다. ('혹은'이라는 표현을 한 것은 어차피 sin으로 표현할 수 있는 것은 모두 cos 함수로 표현할 수 있기 때문이다. )
사인파의 모양을 결정짓는 요인은 3가지다. 파형의 크기를 나타내는 진폭(Amplitude), 파형이 얼마나 빠르게 변하는지를 나타내는 주파수(Frequency), 그리고 파형이 시작되는 지점에서의 모양을 나타내는 위상(Phase)



사인파를 수식으로 어떻게 표현하는지 알아보자.
가장 단순한 식: 각도 θ
각도

진폭(Amplitude) 변화에 대한 식
진폭이 커진다는 것은, 사인 함수의 모든 값이 커진다는 것이다. 2만큼 커진다면 사인 함숫값에 2를 곱하면 된다.
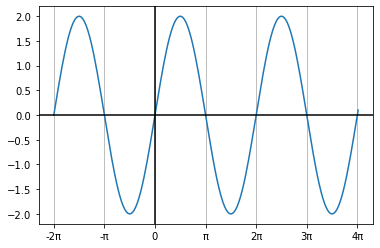
일반화해서, 진폭이 A라면 그때의 사인파의 식은,
| 진폭은 종종 최댓값과 최솟값 사이의 차이로 착각할 수 있는데, 그게 아니고, 파형의 위아래에 대한 중심에서 최고점 혹은 최저점까지의 거리이다. 위 그림에서는 y=0이되는 중심에서 최댓값 2까지가 진폭이다. |
위상(Phase) 변화에 대한 식
답은,
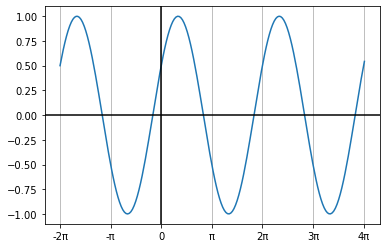
(위 그래프는
이것을 그래프의 이동으로 표현하면,
일반화하면,
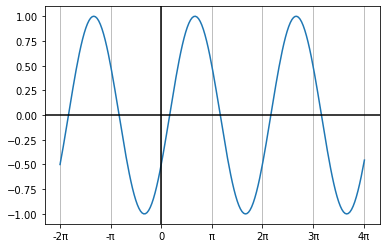
(위 그래프의 식은
주파수(Frequency) 변화에 대한 식
주파수는 단위 시간 동안의 주기 수를 의미하고, 주파수 값이 클수록 주기가 빨리 변한다.
주파수를 각도 변화와 관련해서 생각해보면, 사인 함수의 경우 1주기는 360도이기에, 1초 동안 1번 주기라면, 1초 동안 각도가 0에서 360도로 바뀌었다는 것으로 생각할 수 있다. 즉, 주파수 1이라는 것은 1초 동안 1번의 주기를 보이는 것이고, 이는 1초 동안 각도가 0에서 360도로 변한 것이다.
따라서, 주파수의 변화는 시간당 각도의 변화가 얼마나 빨리 이루어지는가를 나타내는 것이라고도 할 수 있다.
그렇다면 이 주파수가 변한다는 것을 기존
진폭의 변화는
각도
일반적인 속도(
각속도(
따라서, 사인파 식에서
주파수는 시간당 몇 개의 주기가 있느냐이기에, 이를 각도로 표현하면 시간당 360도짜리 회전이 몇 번 있느냐와 같다.
주파수 = 시간당 주기 수 = 시간당 몇 바퀴 회전이 있는가 = 시간당 360도 각도 변화가 몇 번 있는가
따라서, 1 주파수는 360도 각도 변화이고, 각속도는 시간당 각도 변화이기에,
이를 수식으로 나타내면,
위 식에서 360도를
잠시 라디안(radian)에 대해 알아보자.
라디안은
기존의 '도'말고 라디안을 사용하는 이유는, 각도를
| 라디안이라는 것은 비례값이기에 '단위'가 없는 그냥 '수'이다. 따라서, 수학연산에 있어 좀 더 자유롭다. 또한, 라디안 값 따라서, 미분이 필요한 수학이나 자연과학에서는 일반적으로 라디안 표기법을 사용한다. |
그럼 1 라디안은 얼마만큼의 값인가? '도'로 나타내면 약 57.2958이다. 근삿값으로 얘기한 이유는 값이 무리수이기 때문이다. 무리수가 된 이유는 라디안 값의 정의 때문이다.
라디안의 정의는 "원의 반지름
정의가 헷갈리다면 다음과 같이 생각해 본다.
- 원이 있을 때, 원의 반지를
r - 원주 위에 잘라낸 끈을 놓고, 원의 모양대로 구부려서 그 끝을 A와 B라 하자
- 원의 중심 O에서 A와 B로 선을 긋자. 그러면 그 사잇각
∠AOB
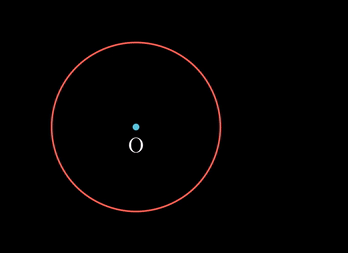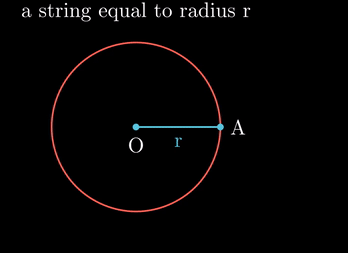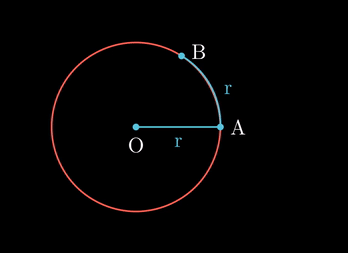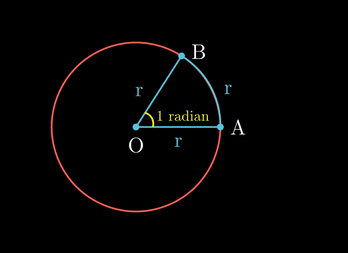
1 라디안을 위와 같이, 반지름 r과 같은 크기의 호를 가질때의 각의 크기로 정했기에, 원의 전체 각도를 라디안으로 나타내면
왜냐하면,
- 원의 둘레를 반지름에 의해 구하면
2πr r 2π - 여기서, 호의 크기가
r r 2π 2π
비례식으로 생각할 수 도 있다.
즉,
어떤 라디안 값
어떤
이제 사인파에 대해 시간당 얼마나 빨리 각이 움직이는가 즉, 시간당 얼마나 빨리 파형이 바뀌는 지를 각속도
여기에, 진폭(A)과 위상차(
| 사인파의 표기는, 각속도 필요에 따라 각각 각속도, 주파수, 주기에 의해 신호를 표현하기 때문이다. |
사인파를 사인함수로 나타내는 것에 익숙해지기 위해서, 몇 개 그래프를 엑셀로 그려보자.
(실습 1) 진폭 1이고, 1초에 2번 주기가 바뀌고, 위상차가 0인 사인파
진폭(A)=1, 주파수(f)=2, 위상차(
이것을 엑셀에서 그려보자.
여기에 사용된 엑셀 파일은,
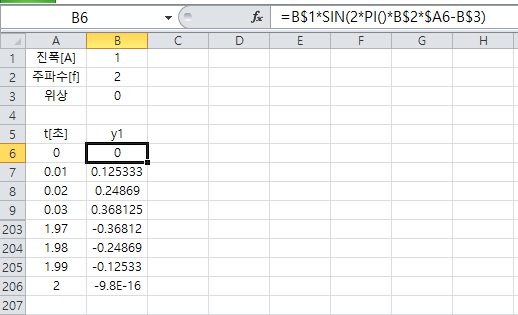
진폭, 주파수, 위상을 입력하고, 시간은 0.01초 간격으로 2초까지 사용한다.
y에 대한 식은
t와 y값이 있는 셀인 A6:B205까지를 선택하고, "곡선이 있는 분산형" 그래프를 그리면 사인 그래프가 생성된다.
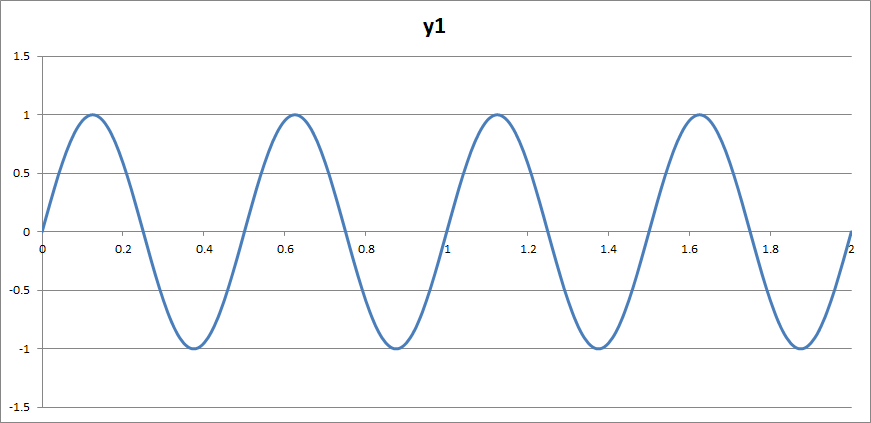
그래프를 보면,
- 진폭이 1이기에, 그래프의 높이가 1이고,
- 주파수가 2이기에, 1초에 2개의 사인파가 그려지고,
- 위상차가 0이기에, t=0에서의 값이 0에서 시작하고 있다.
(실습 2) 진폭 10, 주파수 5, 위상차 −π6
A=10, f=5,
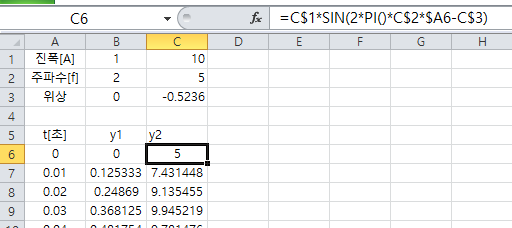
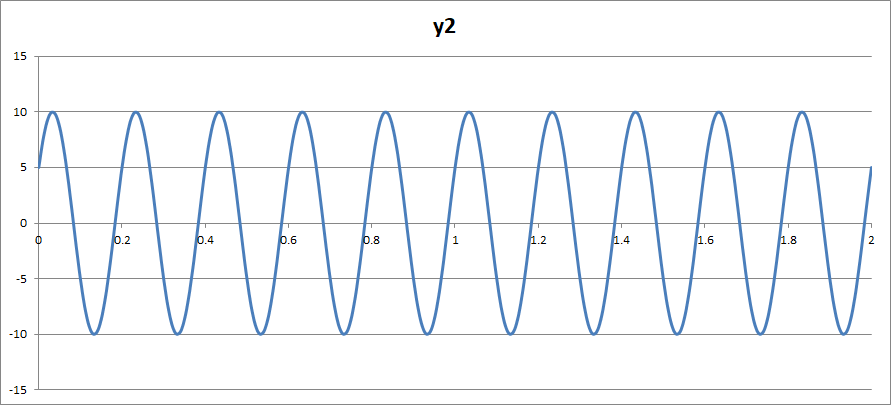
그래프의 높이가 10이고, 1초에 5개의 사인파가 있고, 그래프의 시작이
사인파를 표현하는 방법에 대해 알아봤다.
가장 단순한 주기신호를 사인파로 하기로 했고, 이 사인파를 sine함수를 통해서 할 수 있다는 것을 알았다.
그리고, 사인함수는 진폭(
이제 이 사인파 여러개를 합쳐서 복잡한 신호를 만드는 것에 대해 알아볼 것이다.
-끝-
| 이전글: 02-1. 푸리에 급수 : 주기신호, 삼각 함수(사인, 코사인 그래프) |
| 다음글: 02-3. 푸리에 급수: 사인파의 합을 통해 복잡한 파형 만들기) |
| 다음다음글: 03. 푸리에 계수 |
'푸리에 변환, 신호 > 푸리에 변환의 모든 것' 카테고리의 다른 글
| 04. 푸리에 급수의 복소지수 표현 (0) | 2020.10.11 |
|---|---|
| 03. 푸리에 계수 (10) | 2020.10.04 |
| 02-2. 푸리에 급수: 사인파의 합을 통해 복잡한 파형 만들기 (4) | 2020.10.01 |
| 02. 푸리에 급수 : 주기신호, 삼각 함수(사인, 코사인 그래프) (3) | 2020.09.15 |
| 01. 푸리에 변환이란 (5) | 2020.09.12 |



