이 페이지에서는 DFT를 고속 계산하게 해 주는 쿨리-튜키 알고리즘을 소개한다.
쿨리-튜키 알고리즘은 분할정복(Divide and Conquer)기반 알고리즘이다.
분할정복은
N개의 데이터를
분할 정복 알고리즘
분할정복 알고리즘이 성립하려면, N개의 데이터를
분할 정복 알고리즘을 적용할 수 있는 조건
- 조건 1: 1/2개의 데이터로 나눠서 계산 후 상수 시간 안에 합쳐서 원래 N개일 때의 계산 값으로 도출 가능
- 조건 2: 2개의 데이터에 대해서 상수 시간 안에 계산 가능

N개일 때의 계산량이,
1/2로 분할한 데이터를 다시 또 각각 1/2로 분할하는 것을 계속하면, 끝내는 2개의 데이터에 대해서 계산하는 단계까지 내려갈 것이고, 이 2개의 데이터에 대해서 계산한 것을 이제는 위쪽으로 보내서 합치면서 원래 N일 때의 계산을 수행하게 된다.

이렇게 하게 되면, 분할하는데
DFT에 대한 분할정복 알고리즘 적용
DFT 수식은 위의 분할정복 알고리즘을 적용할 수 있는 2가지 조건을 만족한다.
- 조건 1: 1/2개의 데이터로 나눠서 계산 후 상수 시간 안에 합쳐서 원래 N개일 때의 계산 값으로 도출 가능
- 조건 2: 2개의 데이터에 대해서 상수 시간 안에 계산 가능
위 조건에 맞게끔 DFT의 식을 변형시켜 적용한 것이 쿨리-튜키 알고리즘이다.
DFT 식으로부터 분할정복 형태가 되도록 유도해보자.
먼저 길이 N인 y(n) 데이터를 2개로 나눠보자. 여기서 N은 짝수로 가정.
하나는 n이 짝수인 것, 그리고 다른 하나는 홀수로 나누면 정확하게 2개로 나눌 수 있을 것이다. (DFT 수식에 사용된 W 함수가 짝수, 홀수에 따라 구분되는 특성이 있기에 짝/홀수로 나누는 것임)

짝수로 구성된 것을
이제 N개의 원소를 가진 데이터 y(n)의 DFT식을 p(n)과 q(n)을 이용해서 표현하면,
식(2)에서 유도된 제일 마지막 식을 보면,
즉, N개 데이터에 대한 DFT식이,
식의 유도과정을 좀 더 자세히 보자.
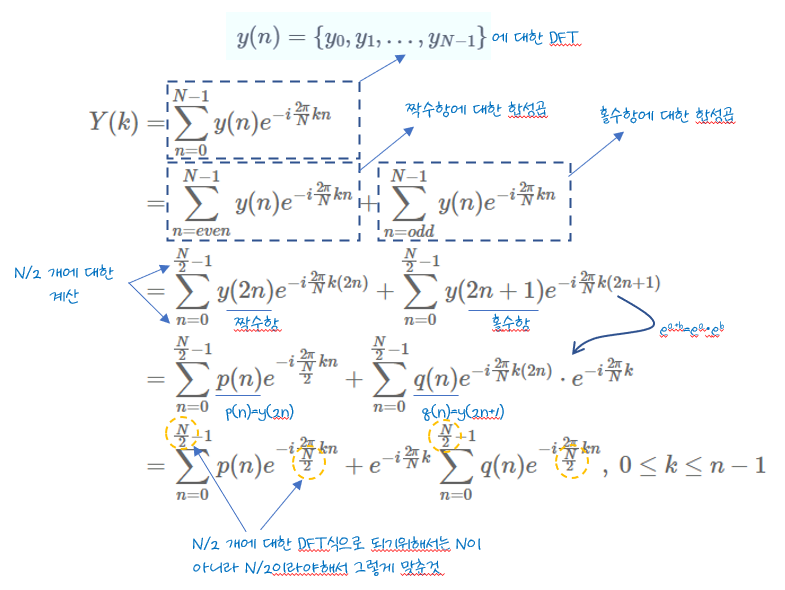
그런데, (식 2) 및 (식 3)이 왜 계산량을 적게 하는지, 그리고 왜 이렇게 나눈 것이 의미가 있는 걸까?
(식 3)에서
(식 4)에서는 총 N번의 곱셈 연산과 N번의 덧셈 연산이 일어난다. Y(0) 계산을 위해 1번씩, Y(1)을 위해 1번... 이렇게 Y(7)까지 구하려면 N번의 곱셈과 N번의 덧셈을 하면 된다.
알고리즘의 연산량을 계산할 때 N+N은 그냥
즉, N개에 원소에 대해서 2로 나눴을 때 연산량이 N회 발생.
이제 P와 Q를 구하기 위해서, P와 Q를 각각 절반으로 나눠서 계산하자. P를 절반으로 나는 것을 A, B라 하고, Q를 절반으로 나는 것을 C, D라고 하면,
P와 Q를 구하기 위해서도 역시 N번의 연산이 필요.
이러한 과정을 원소가 2개가 될 때까지 계속하게 되고, 원소가 2개씩 남았을 때도 역시 N번의 연산 필요.
N에서부터 시작해서 2개씩 나눠서 최종 원소가 2개 남을 때까지 수행되는 횟수는
따라서, 전체 연산 횟수는
(식 3)에서, DFT값의 주기성과 복소지수함수의 성질을 이용하면, 좀 더 단순화시켜서
(식 3)에서 P(k)와 Q(k)는 각각
따라서,
또한 복소지수함수의 성질에 의해서
(
이제 (식 3)을 다음과 같이 쓸 수 있다.
(식 4)에서
(식 5)에 대해서 N=8의 경우를 예로 들어보자.
Y(0)~Y(3)까지는 (식 5)의 윗 식을, Y(4)~Y(7)까지는 (식 5)의 아랫 식을 이용한 것이다.
즉, Y(0)~Y(7)까지의 값을 4개의 P, W, Q값을 가지고 계산할 수 있는 것이다.
위 식을 보면 대칭적인 규칙을 가지고 있다.
그래프로 그려보면 그 규칙이 잘 보인다.
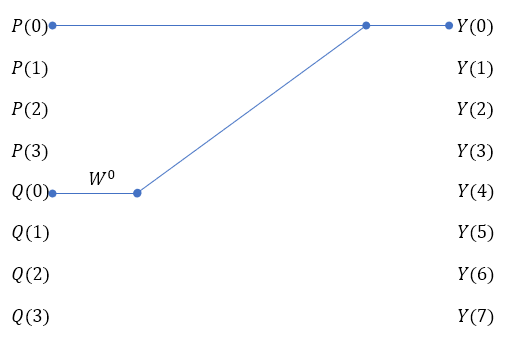
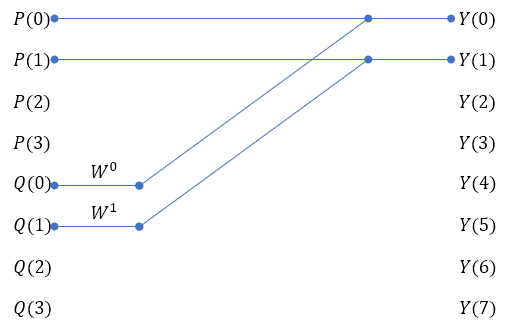
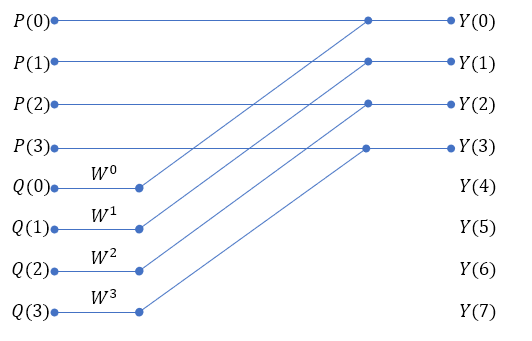
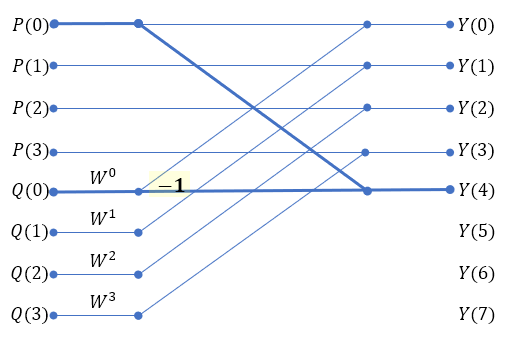
이제 남은 Y(5)~Y(7)까지를 다 그려 넣으면,
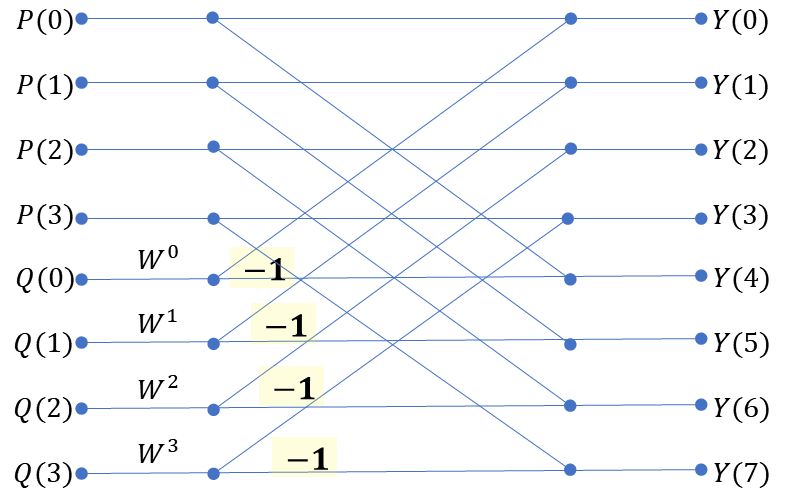
이제
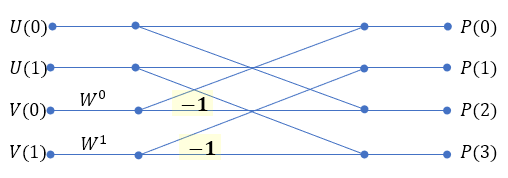
마찬가지로
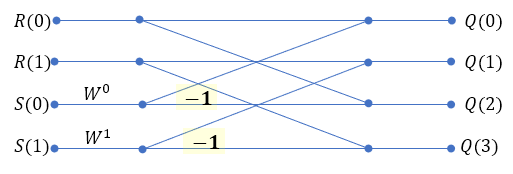
이제
2개 데이터를 이용해서 DFT 값을 구하는 것은, 실제 DFT 식에 넣어보면 굉장히 단순한 실수연산으로 변환이 된다.
길이가 2인 x(n)에 대한 DFT 값 X(k)를 구하는 것을 생각해보자. DFT식은,
여기서
정리하면,
2개 포인트에 대한 DFT 계산은, 이처럼 두 개 값의 덧셈과 뺄셈으로 간단히 계산될 수 있다.
이처럼, 8개 데이터에 대한 FFT의 최종 값 Y(k)의 계산은,
- 3단계: Y(k) 값은, 4 포인트에 대한 FFT값인 P(k)와 Q(k)에 의해서 계산되고,
- 2단계: P(k)와 Q(k)는, 2 포인트에 대한 FFT 값인 U(k), V(k), R(k), S(k)에 의해 계산되고,
- 1단계: U(k), V(k), R(k), S(k)는, 원래 주어진 y(n)에 의해 계산된다.
실제 계산을 할 때 제일 아랫단에서의 y(n)에 의해 U(k), V(k), R(k), S(k)를 구하는 것이 제일 먼저 진행되기 때문에, 이 과정을 1단계로 표현한 것임
(식 5)가 FFT의 수식이고 알고리즘의 전부다.
식만 봐서는 어떻게 계산되는지 감이 잘 안 잡히고, 위에서 8개 포인트의 데이터에 대한 수식을 예로 들었으나, 아직 완벽하게 이해되지 않을 수 있다.
실제 8개 포인트 데이터에 대한 FFT 계산을 손으로 한 단계씩 계산해보면, 어떻게 계산이 되는지 체득할 수 있을 것이다. 다음 페이지에서 그렇게 계산해볼 것이다.
-끝-
| 이전글: 07. FFT (Fast Fourier Transform, 고속 푸리에 변환) |
| 다음글: 07-2. FFT 예제를 손으로 풀어보며 이해하기 |
| 다음다음글: 07-3. 엑셀에서 FFT 계산하기 (엑셀 자체 FFT 기능) |
'푸리에 변환, 신호 > 푸리에 변환의 모든 것' 카테고리의 다른 글
| 07-3. 엑셀에서 FFT 계산하기 (엑셀 자체 FFT 기능) (0) | 2022.07.28 |
|---|---|
| 07-2. FFT 예제를 손으로 풀어보며 이해하기 (5) | 2022.07.28 |
| 07. FFT (Fast Fourier Transform, 고속 푸리에 변환) (0) | 2022.07.24 |
| 06-7. 엑셀을 이용한 DFT 계산(4/4) (0) | 2022.07.24 |
| 06-6. 엑셀을 이용한 DFT 계산(3/4) (0) | 2022.07.23 |



