$y(n)={0,0,0,0,1,1,1,1}$인 값에 대해 FFT 수식을 이용해서 단계별로 손으로 문제를 풀듯이 계산해보자.
먼저 이 값을 DFT 수식을 이용해서 엑셀에서 구해보면 다음과 같다.
$$ DFT: \; \; Y(k)=\sum_{n=0}^{N-1}{y(n)e^{-i\frac{2\pi}{N}kn}}, \; \; 0\leq k < N \tag {1} $$
$$ IDFT: \; \; y(n) = \frac{1}{N} \sum_{k=0}^{N-1}Y(k) e^{i\frac{2\pi}{N}kn}, \; \; 0 \le n < N \tag{2} $$

FFT를 이용해서 구해보자. FFT의 수식은,
$$ \begin{align}Y(k) = P(k) + W^kQ(k), \; &0 \le k \le {\frac{N}{2}-1} \\ Y(k+\frac{N}{2})=P(k)-W^kQ(k), \; &0 \le k \le {\frac{N}{2}-1} \tag{5} \end{align} $$
8개 포인트 데이터에 대해서 구할 때, FFT에서는 아래 이미지와 같은 순서로 구해진다.
- P와 Q에 의해서 --> Y가 구해지고,
- U, V, R, S에 의해서 -> P, Q가 구해지고,
- y(n)에 의해서 --> U, V, R, S가 구해진다.
여기서 P, Q, U, .. 등은 임의로 붙인 기호이고, 기호 이름 자체에 큰 의미는 없다. 주어진 y(n) 데이터에 의해 2 포인트 DFT값이 구해지고, 2포인트 DFT 값에 의해서 4 포인트의 DFT가 구해지는 관계만 이해하면 된다.

(그림 2)에서 y(n)의 번호가 0~7까지 순서대로 되어 있지 않음에 유의한다.
왜 이렇게 되었을까?
최종 결괏값 Y(k)의 관점에서 생각해보자.
Y(k)의 경우는 0~7까지 차례대로 되어 있다.
그렇다면, y(n)에서 직접 Y(k)를 계산한다면(DFT를 이용해서), y(n)도 0~7까지 차례대로인 상태일 것이다.
그런데, FFT에서는 짝수항인 {y(0), y(2), y(4), y(6)}을 P로 놨고, 홀수항 {y(1), y(3), y(5), y(7)}을 Q로 놓고서 계산한다.
따라서,
$$ \begin{align} &p(0) = y{0} \\ &p(1) = y{2} \\ &p(2) = y{4} \\ &p(3) = y{6} \\ \\ &q(0) = y{2} \\ &q(1) = y{4} \\ &q(2) = y{4} \\ &q(3) = y{7} \end{align}$$
개념도에 표시해보면 아래와 같이 될 것이다.

이제 P와 Q를 구하는 것에 대해 생각해보자.
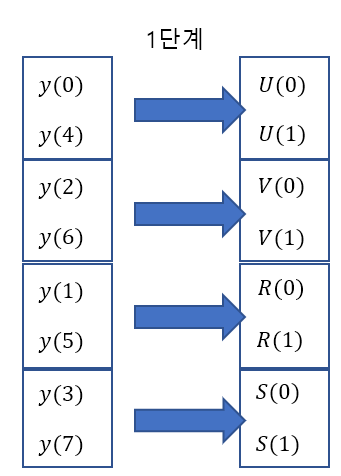
먼저 P에 대해서는, 짝수항에 의한 FFT값인 U와, 홀수항에 의한 FFT값인 V에 의해서 구해진다. 여기서 짝수항은 (그림 3)에서 노란색을 칠한 값들이다. 따라서, U값을 구할 때 사용된 y(n)값은 {y(0), y(4)}가 되고, V값을 구하는데 사용되는 y(n)값은 {y(2), y(6)}이 된다. 마찬가지 원리로 R과 S를 구할 때 사용되는 y(n)값을 구할 수 있고, 이를 개념도에 표시해보면 아래와 같다.

(그림 4)를 보면, 처음 1단계 계산을 할 때 어떤 y(n) 값을 사용해야 할지를 알 수 있고, 이것이 (그림 2)에서 y(n)의 순서를 이러한 순서로 놓은 이유이다.
포인트가 8개일 때야 단계가 3단계밖에 안되기에 손으로 y(n)의 계산 순서를 정할 수 있지만, y(n)이 수백수천 개의 포인트일 때는 이러한 방법으로 y(n)의 계산 순서를 정할 순 없다.
FFT를 프로그래밍할 때는 이러한 수동 방법을 쓰지 않고, 쉽게 y(n)의 순서를 정하는 알고리즘을 사용한다. 이 알고리즘은 다음 페이지에서 엑셀 VBA를 사용한 FFT 프로그래밍에서 소개할 것이다.
이제 FFT를 어떻게 구해야 할지 스케치는 되었고, 실제 계산을 해보자.
계산 순서는 다음과 같다.
- [1단계] 계산 수행 : $A(0)=a(0)+a(1), A(1)=a(0)-a(1)$ 이용
- [2단계] 계산 수행: $\{W_4^0, W_4^1\}$을 구하고, N=4일 때의 FFT 수식 이용
- [3단계] 계산 수행: $\{W_8^0, W_8^1, W_8^2, W_8^3\}$을 구하고, N=8일때의 FFT 수식 이용
각 단계별 계산을 하기에 앞서 W를 구하는 방법을 먼저 알아보자.
$W^k$의 계산
N=8이라면 $W_8^k=e^{-i\frac{2\pi}{8}k}=e^{-i\frac{\pi}{4}k}=\cos{\frac{k\pi}{4}}-i\sin{\frac{k\pi}{4}}$
계산해보면, ($N_8^k$에서 밑 수 8은 생략해서 표현하자. 복잡함을 피하기 위해)
$$ \begin{align} &W^0=\cos{\frac{0\cdot \pi}{4}}-i\sin{\frac{0 \cdot \pi}{4}} = 1-i\cdot 0 = 1 \\ &W^1=\cos{\frac{1\cdot \pi}{4}}-i\sin{\frac{1 \cdot \pi}{4}} = \frac{1}{\sqrt{2}}-i\frac{1}{\sqrt{2}}=0.71-0.71i \\ &W^2=\cos{\frac{2\cdot \pi}{4}}-i\sin{\frac{2 \cdot \pi}{4}}=\cos{\frac{\pi}{2}}-i\sin{\frac{\pi}{2}}=0-i=-i \\ &W^3=\cos{\frac{3\cdot \pi}{4}}-i\sin{\frac{3 \cdot \pi}{4}} = -\frac{1}{\sqrt{2}}-i\frac{1}{\sqrt{2}}=-0.71-0.71i \end{align}$$
$W_N^k$ 값을 이렇게 오일러 공식으로 삼각함수로 변환 후 손으로 계산할 수도 있으나, 복소평면에서의 그림으로 생각하면 더 쉽게 계산될 수 있다.
N=8이기에, $W_8^k$의 값은 복소평면에서 반지름이 1인 원에서 360도를 8 등분한 지점의 값이고, $W_8^0$~$W_8^4$의 값은 실수 측 1에서 시작해서 반시계 방향으로의 4개 포인트에서의 복소 값이다.
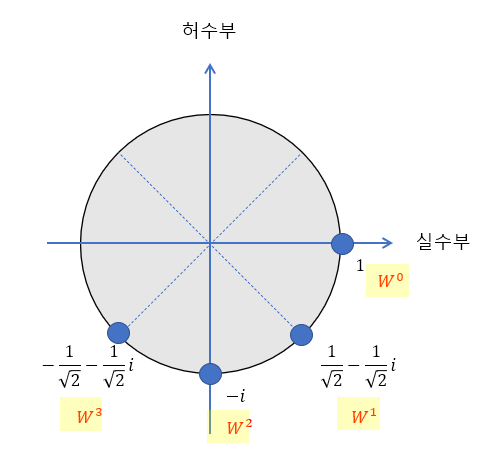
여하튼, $N=8$일 때 $W^k$의 값은,
| $W^0$ | $1$ |
| $W^1$ | $0.71-0.71i$ |
| $W^2$ | $-i$ |
| $W^3$ | $-0.71i-0.71i$ |
마찬가지로 계산하면 $N=4$일 때의 $W^k$의 값은,
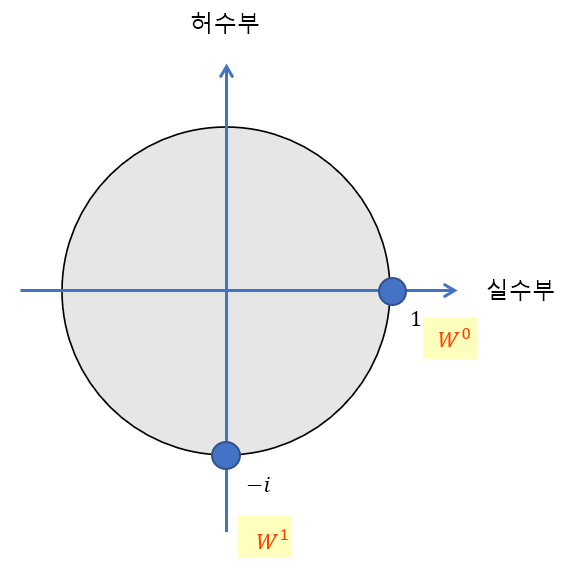
| $W^0$ | $1$ |
| $W^1$ | $-i$ |
[1단계] 계산
1단계는 y(n)의 2개의 쌍으로부터 직접 값을 구한다.
공식은,
$$ \begin{align} &A(0)=a(0)+a(1) \\ &A(1)=a(0)- a(1)\end{align}$$
위 공식에 따라 계산을 해보자.
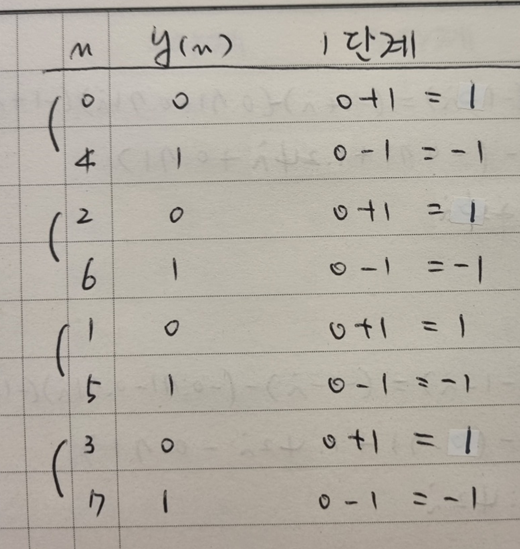
[2단계] 계산
2단계는 1단계의 계산 결과를 가지고, N=4일 때의 계산을 하면 된다.
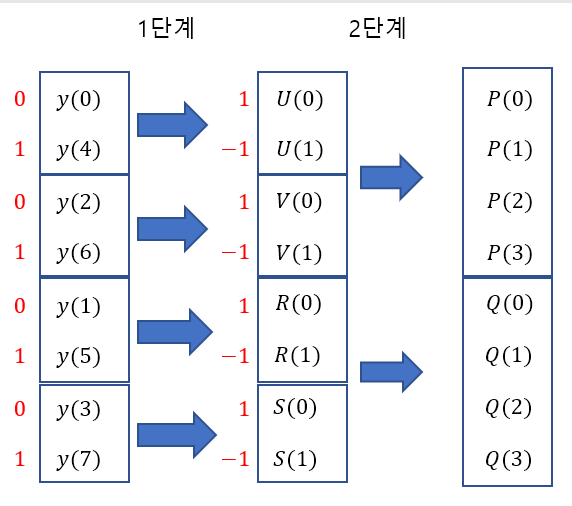
N=4일 때의 계산 방법은,
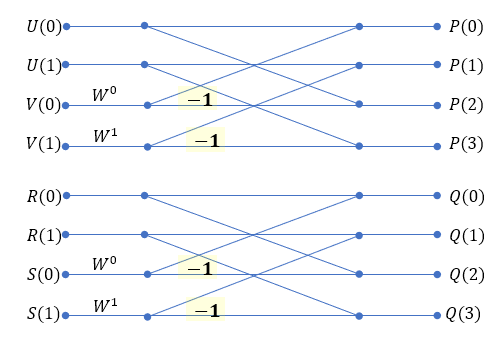
위 계산방법에 따라 계산을 하면 아래와 같다.

위 풀이식에서, 아랫부분 4개는, 윗부분 4개와 같은 값에서 유도되는 것이기에, 다시 계산할 필요 없이, 똑같은 결과일 것이기에 다시 계산하지 않은 것이다.
그리고, N=4이기에 $W_4^k$의 값을 사용한다.
[3단계 계산]
3단계 계산은 2단계의 결과를 가지고 계산한다.
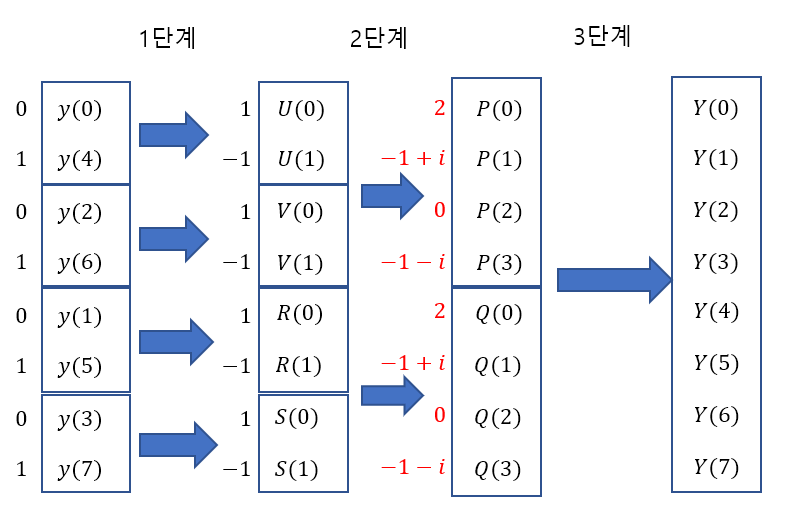
이때 계산되는 FFT 수식은 N=8일 때의 수식이다.
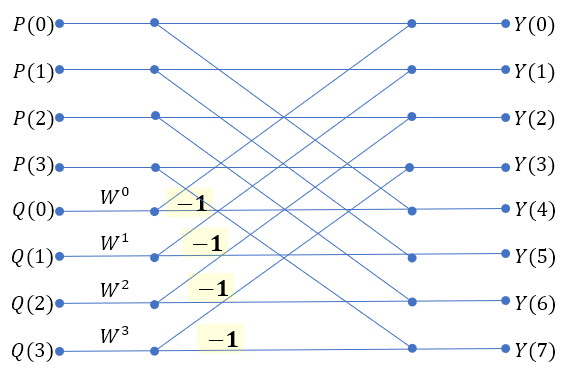
계산해보면 아래와 같이 된다.

위 계산에서, Y(1), Y(3), Y(5), Y(7)에 대한 계산은, 식이 복잡하여 따로 계산식을 적는다.
Y(1) 계산은,

Y(3)의 계산은,

Y(5)의 계산은,
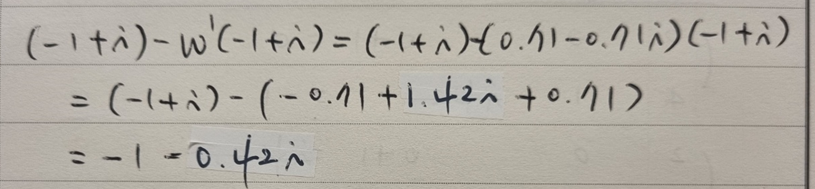
Y(7)의 계산은,
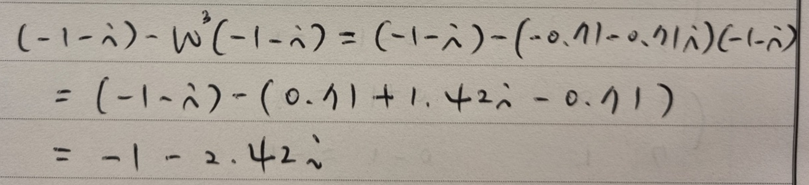
이처럼 FFT에 의한 계산 결과를 (그림 1)의 DFT를 이용한 결과와 비교해보면, 일치함을 알 수 있다.
FFT 프로그램에서는 위에서 손으로 구한 방법처럼 계산이 진행되고, 이렇게 하면 $O(N\log{N})$ 연산 시간에 푸리에 변환 값을 구할 수 있다.
다음 페이지부터는, 엑셀 자체 기능으로 있는 FFT함수의 사용 및 직접 FFT를 프로그래밍하는 것을 해볼 것이다.
-끝-
| 이전글: 07-1. FFT의 유도 |
| 다음글: 07-3. 엑셀에서 FFT 계산하기 (엑셀 자체 FFT 기능) |
| 다음다음글: 07-4. 엑셀에서 직접 FFT 프로그래밍 작성하기 |
'푸리에 변환, 신호 > 푸리에 변환의 모든 것' 카테고리의 다른 글
| 07-4. 엑셀에서 직접 FFT 프로그램 만들기 (7) | 2022.07.28 |
|---|---|
| 07-3. 엑셀에서 FFT 계산하기 (엑셀 자체 FFT 기능) (0) | 2022.07.28 |
| 07-1. FFT 유도 (9) | 2022.07.25 |
| 07. FFT (Fast Fourier Transform, 고속 푸리에 변환) (0) | 2022.07.24 |
| 06-7. 엑셀을 이용한 DFT 계산(4/4) (0) | 2022.07.24 |



