[예제 4] N값을 크게 해서 주파수 분해능을 높이기
두 개의 코사인 파가 합쳐진 신호를 가지고 분석해 볼 것이다.
- 신호 수식: 1 kHz와 1.1kHz의 정현파가 합쳐진 신호 --> $\cos{2\pi \cdot 1000t} + \cos{2\pi \cdot 1100t}$
- 샘플링 주파수($f_s$): 8kHz
- y(n)에 대한 수식: =ROUND(COS(2*PI()*(1/8)*B14)+COS(2*PI()*(11/80)*B14),2)


주파수 샘플링에 대한 주기 N=32로 해서 계산해보자.
W(n,k)를 구하기 위해 셀 "E14"에 수식을 적고, 자동채우기로 나머지 셀에 대해서도 값을 구한다.
- 셀 "E14"의 수식: =ROUND(COS(2*PI()*(1/8)*B14)+COS(2*PI()*(11/80)*B14),2)

이제 Y(k)를 구해보면,
- Y(k) --> 셀 "E46" 수식: =CSumProduct($C14:$C45,E14:E45)
- Y(k)_re --> 셀 "E47" 수식: =IMREAL(E46)
- Y(k)_im --> 셀 "E48" 수식: =IMAGINARY(E46)
- Y(k)_magnitude --> 셀 "E49" 수식: =ROUND(SQRT(E47^2+E48^2),2)

Y(k)_magnitude에 대해 그래프를 그려보면, Y(4)에 대한 값이 크고, Y(5)의 값도 조금 크게 그려진다.

k에 대한 주파수 분해능을 생각해보면(k의 간격), 샘플링 주파수 $f_s=8kHz$이고 $N=32$이기에, k의 분해능은 $\frac{8k}{32}Hz = 250Hz$이다.
따라서,
- k=4: $4 \cdot 250 = 1000 Hz$
- k=5: $5 \cdot 250 = 1250 Hz$
즉, DFT를 한 결과, 1000Hz의 신호가 대부분이고, 1250Hz의 성분도 조금 있다고 해석되고, 이것은, 원래의 신호가 1000Hz와 1100Hz로 구성되어 있기에, 오차가 큰 해석이다.
이러한 오차가 발생한 이유는 주파수의 분해능이 세밀하지 않아서이다.
원래의 신호 간의 주파수 차이가 100Hz인데 (100Hz = 1100Hz - 1000Hz), N=32에 의한 k의 분해능이 250Hz이기에, 세밀하게 주파수 차이를 구분하지 못하기 때문이다.
k의 간격을 더 세밀하게 하기 위해 N의 값을 크게 하고(32 --> 128), y(n)의 값도 더 많아지게 해 보자.
변경 사항은,
| 항목 | 변경 전 | 변경 후 |
| y(n) 범위 | y[0] ~ y[31] | y[0] ~ y[127] |
| N | 32 | 128 |
| k 범위 | 0~31 | 0~127 |
| Y(k) 계산 범위 | Y[0]~Y[31] | Y[0]~Y[127] |
이렇게 해서 Y(k)를 구하고, 그 크기에 대해 그래프를 그려보면, Y[16]과 Y[189]의 값의 크게 나온다. (그래프의 오른편 끝 쪽의 Y[110], Y[112]는 Y[16]과 Y[18]와 대칭이되는 주파수 값이기에, Y[16]과 Y[18]에 대해서만 얘기해도 되겠다.)
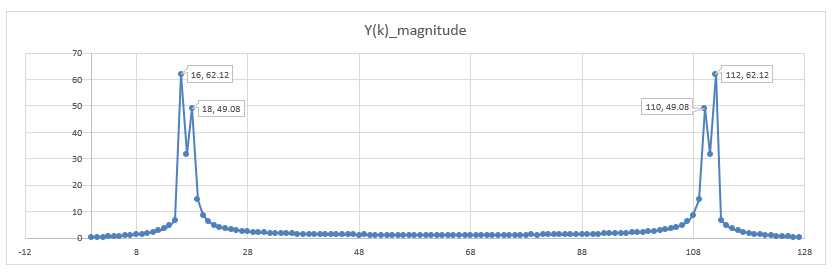
N=128이고 $f_s=8 kHz$이기에, k의 분해능은 $\frac{8000Hz}{128}=62.5Hz$이다.
따라서,
- k=16: $16 \times 62.5 = 1000 Hz $
- k=18: $18 \times 62.5 = 1125.5 Hz $
즉, 신호가 1000Hz와 1125.5Hz로 구성되었다고 해석할 수 있는 것이고, 원래의 신호가 1000Hz와 1100Hz이기에 25.5Hz의 오차가 있지만, 앞에서 N=32일 때보다 훨씬 오차의 크기가 작아졌다.
이것은 N의 크기를 크게 했기에 DFT의 결과인 Y(k)에서의 k의 간격이 촘촘해져서, 세밀한 주파수 차이를 감지할 수 있는 것이다.
이렇게 N을 크게 하면 DFT의 결과에서, 촘촘한 간격으로 주파수 성분을 해석할 수 있다. 그러나, N을 크게 할수록 계산해야 하는 데이터의 개수가 늘어나기에, 계산량은 더 많아진다. Y(k)를 구할 때 합성곱의 범위가 n=0에서 N-1까지의 범위이기에, N이 커질수록 합성곱을해야할 계산량이 많아지는 것이다.
위의 경우는 k의 주파수 분해능을 높이기 위해서(세밀한 주파수 분석을 위해서) N의 값을 크게 했고, 이에 따라 y(n)의 값도 0~(N-1)까지의 값이 필요하기에, y(n)의 값을 신호수식에 의해 구한 후 사용했다.
그런데 만약 y(n)의 값이 적다면 어떻게 해야 할까? 주파수 분해능을 더 올릴 수 없는 것인가?
예를 들어 y(n)의 값이 y[0]~y[31]까지만 존재한다면, N=32로 할 수밖에 없다.
N=64로 크게 하려면, y[32]~y[63]까지의 값이 추가로 필요하기 때문이다.
그렇다면, 사용할 수 있는 N의 최댓값이 32라면, 샘플링 주파수가 8kHz의 경우 k의 주파수 분해능은 250Hz가 최대일 것이다. ( $\frac{8k}{32}Hz = 250Hz$ )
그러나, 이처럼 y(n)의 값이 적게 있더라도 주파수 분해능을 어느 정도 높일 수 있다.
만약 y[0]~y[31]까지만 값이 있는 경우, y[32]~y[63]까지의 값을 0으로 넣고 N=64로해서 계산하면 k의 주파수 분해능을 높일 수 있다.
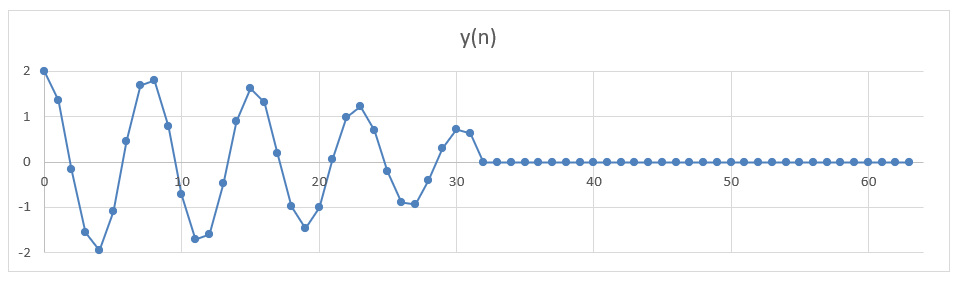
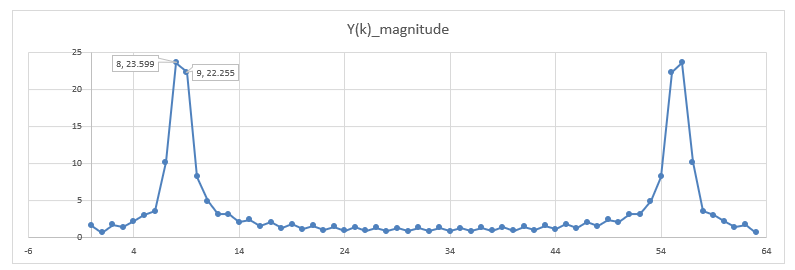
위 그래프와 같이 y[32]~y[63]까지의 값을 0으로 처리하고, DFT를 수행해서 Y(k)를 구해보면, 아래 그래프와 같이 Y[8]과 Y[9]에서 큰 값을 보이고 있어서, N=32로 했을 때 보다 더 원래의 신호값에 유사한 특성을 보여준다.
- k=8: $8 \times \frac{8000}{64}Hz = 1000Hz$
- k=9: $9 \times \frac{8000}{64}Hz = 1125Hz$
이 페이지에서 사용된 엑셀 파일:
- 끝 -
| 이전글: 06-6. 엑셀을 이용한 DFT 계산(3/4) |
| 다음글: 06-8. DFT 수식에 대한 해석 --> 작성중 |
| 다음다음글: 07. FFT (Fast Fourier Transform, 고속 푸리에 변환) |
'푸리에 변환, 신호 > 푸리에 변환의 모든 것' 카테고리의 다른 글
| 07-1. FFT 유도 (9) | 2022.07.25 |
|---|---|
| 07. FFT (Fast Fourier Transform, 고속 푸리에 변환) (0) | 2022.07.24 |
| 06-6. 엑셀을 이용한 DFT 계산(3/4) (0) | 2022.07.23 |
| 06-5. 엑셀을 이용한 DFT 계산(2/4) (3) | 2022.07.22 |
| 06-4. 엑셀을 이용한 DFT 계산(1/4) (0) | 2022.07.11 |



