04-3. 매클로린 급수, 오일러 공식

앞 챕터들에서 복소평면에서의 원의 함수 식, 그리고 복소 지수함수와 그에 대한 미분에 대해 알아봤다.

 

  원의 함수 식: $\cos x+i\sin x$

  복소 지수 함수: $e^{ix}$ 

 

이제 이 둘이 만날 차례이다. 즉, 복소평면에서의 원의 함수 식과 복소 지수로 표현된 $e^{ix}$가 같음을 보일 것이다. 

그 수단으로는 매클로린 급수를 사용할 것이다.

 

---

매클로린 급수

매클로린 급수(Maclaurin's series) 혹은 매클로린 전개로 불리는 것은, 아래와 같은 형태의 식으로, 어떠한 함수라도(사인 함수, 지수 함수 등 어떠한 함수라도) 이러한 다항식 형태로 표현할 수 있다고 한다.

 

    $$f(x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+a_4{x}^4+a_5{x}^5+a_6{x}^6+...(식1)$$   

 

위 식을 합을 표현하는 기호인 시그마($\sum$)를 이용해서 쓰면,

    $$f(x)=\sum _{n=0}^{\mathrm{\infty }}{a}_n{x}^n(식2)$$ 

 

 

예를 들어, $f(x)=4x^4+2x^2+3x+1$을 매클로린 급수로 표현하면, 

 

    $f(x)=4x^4+2x^2+3x+1=1+3x+2x^2+0\cdot x^3+4x^4$ 

 

따라서 $a_0,a_1$ 등 계수로만 급수를 표현하면,

    $\{a_1,a_1,a_2,a_3,a_4\}=\{1,3,2,0,4\}$

 

 

---

다항식의 경우는 이처럼 쉽게 그 계수를 구할 수 있을 것 같은데, 사인 함수나 지수함수는 어떻게 계수를 정해야 할지 한눈에 안 보인다. 

 

계수를 구하는 방법을 생각해보자.

 

$a_0$부터 시작해서 차례로 어떻게 구할지 알아볼 것이다.

 

예를 들어 $f(x)=\sin x$라고 하면, 이것을 매클로린 급수로 표현할 때 각 계수가 어떻게 될지를 구하는 것이다. 따라서 원래의 함수 $f(x)$는 알고 있고, 이 함수에 어떤 값, 예를 들어 $0$을 대입했을 때의 값 등을 알 수 있는 상태라는 것에 유의. 즉, 원래의 함수에 어떤 조작을하고 값을 대입시켜서, 매클로린 형태일 때의 계수값들을 알아내는 것이 핵심.

 

$a_0$ 구하기

 

(식 1)을 보면 $a_0$를 제외하고 모두 $x$ 혹은 $x$의 지수승이 곱해져 있다. 

 

따라서, $x=0$을 대입시키면 $a_0$값만 남게 될 것이다. 즉, $a_0$값은 원래의 함수 식에 대해 $f(0)$를 해보면 된다.

 

    $f(0)=a_0$

 

$a_1$ 구하기

(식 1)을 다시 한번 써보자

 

    $f(x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+a_4{x}^4+a_5{x}^5+a_6{x}^6+...$   (식 1)

 

$a_0$만 빼고 나머지는 $x$가 곱해진 것을 이용해서 $a_0$를 구했었다.  즉, 모두 $x$와의 곱이니깐, x에다가 0을 집어넣으면 모두가 0이 되는 것을 이용했었다.  $a_1$도 그런 방법을 쓰면 되지 않을까? 

그러려면 $f(x)$를 한 번 미분하면 되겠다. 한 번 미분하면 $a_0$는 0이 되고, $a_{1}x$는 $a_1$이 되고, 나머지는 $x$가 남아 있을 테니깐, 그 상태에서 $0$을 집어넣으면 $a_1$을 구할 수 있을 것이다.

 

    $f^{\prime }(x)=a_1+2a_{2}x+3a_3{x}^2+4a_4{x}^3+5a_{5}x4+6a_6{x}^5+...$

    $f^{\prime }(0)=a_1$

 

즉, $a_1$은 원래의 함수 $f(x)$를 한 번 미분한 후 $x=0$을 입력하면 구해진다. 

 

$(a{x}^b)$에 대한 미분을 하면, $(a{x}^b{)}^{\prime }=ab{x}^{(b-1)}$이다.

$a_2,a_3,...$구하기

 

$a_1$을 구하기 위해서 $f^{\prime }(x)$을 하면 $a_1$만 남게 되어 구할 수 있었다.

같은 원리로, $f(x)$를 두 번, 세 번, 네 번 미분을 하고선 $x=0$을 대입하면, 각각 $a_2,a_3,a_4$를 구할 수 있을 것이다.

 

$f(x)$에 대한 1차, 2차, 3차, 4차,... 미분을 해보자. (4차 미분부터는 괄호 안의 숫자로 미분 차수를 표현했다.)

 

    $f(x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+a_4{x}^4+a_5{x}^5+a_6{x}^6+...$

    $f^{\prime }(x)=a_1+2a_{2}x+3a_3{x}^2+4a_4{x}^3+5a_5{x}^4+6a_6{x}^5+...$

    $f^{″}(x)=2a_2+(3\cdot 2)a_{3}x+(4\cdot 3)a_4{x}^2+(5\cdot 4)a_5{x}^3+(6\cdot 5)a_6{x}^4+...$

    $f^{‴}(x)=(3\cdot 2)a_3+(4\cdot 3\cdot 2)a_{4}x+(5\cdot 4\cdot 3)a_5{x}^2+(6\cdot 5\cdot 4)a_6{x}^3+...$

    $f^{(4)}(x)=(4\cdot 3\cdot 2)a_4+(5\cdot 4\cdot 3\cdot 2)a_{5}x+(6\cdot 5\cdot 4\cdot 3)a_6{x}^2+...$

    $f^{(5)}(x)=(5\cdot 4\cdot 3\cdot 2)a_5+(6\cdot 5\cdot 4\cdot 3\cdot 2)a_{6}x+...$

    $f^{(6)}(x)=(6\cdot 5\cdot 4\cdot 3\cdot 2)a_6+...$

 

각 미분식에 $x=0$을 넣어보면,

    $f(0)=a_0$

    $f^{\prime }(0)=a_1$

    $f^{″}(0)=2a_2$

    $f^{‴}(0)=(3\cdot 2)a_3$

    $f^{(4)}(0)=(4\cdot 3\cdot 2)a_4$

    $f^{(5)}(0)=(5\cdot 4\cdot 3\cdot 2)a_5$

    $f^{(6)}(0)=(6\cdot 5\cdot 4\cdot 3\cdot 2)a_6$

 

뭔가 규칙성이 보인다. 위 식을 각 계수를 구하는 식으로 바꿔보면,

    $a_0=f(0)$

    $a_1=f^{\prime }(0)$

    $a_2=f^{″}(0)/2$

    $a_3=f^{‴}(0)/(3\cdot 2)$

    $a_4=f^{(4)}(0)/(4\cdot 3\cdot 2)$

    $a_5=f^{(5)}(0)/(5\cdot 4\cdot 3\cdot 2)$

    $a_6=f^{(6)}(0)/(6\cdot 5\cdot 4\cdot 3\cdot 2)$

 

여기서 연속된 수의 곱을 팩토리얼(!)을 이용해서 표현하면, 

    $a_0=f(0)$

    $a_1=f^{\prime }(0)$

    $a_2=f^{″}(0)/2!$

    $a_3=f^{‴}(0)/3!$

    $a_4=f^{(4)}(0)/4!$

    $a_5=f^{(5)}(0)/5!$

    $a_6=f^{(6)}(0)/6!$

    ...

    $a_n=f^{(n)}(0)/n!$

 

$n!$은 n에서부터 1까지의 연속된 수의 곱이다. $n!=n\times (n-1)\times (n-2)\times ...\times 2\times 1$ 물론 맨 마직막의 $1$은 곱하지 않아도 되기 때문에 $2$까지만 곱하는 것으로 표현해도 된다.

 

이제 매클로린 급수의 각 계수를 구할 수 있는 일반식을 얻었다. 각 계수는 자신의 차수만큼을 미분한 것에 $0$을 대입하고, 그 값을 차수분 만큼의 팩토리얼로 나눠주면 된다. 

 

$$a_n=\frac{f^{(n)}(0)}{n!}$$

 

앞 쪽 챕터에서, 푸리에 급수의 계수를 구하는 과정과 비슷한 느낌이 들지 않는가? 그 때에는 각 계수와 결합되어 있던 사인 혹은 코사인 값을 곱한 후 적분을 해서 각 계수를 구했다. 여기서는 적분대신에 미분을 사용하고 0을 대입시켜서 구했는데, 좀 다르면서도 구하는 패턴이 비슷하다.

 

---

매클로린 급수에 대해 정리해보자. 

 

어떠한 함수 식이라도 다항식으로 표현할 수 있는 매클로린 급수는 다음과 같다. 

 

$$f(x)=\sum _{n=0}^{\mathrm{\infty }}{a}_n{x}^n(식3)$$ 

 

이때 계수 $a_n$은 다음과 같은 식으로 구할 수 있다.

 

$$a_n=\frac{f^{(n)}(0)}{n!}(식4)$$

 

---

복소평면 위 원의 방정식에 대한 매클로린 전개

 

앞 쪽에 있는 챕터인 04-1. 복소 평면, 복소평면에서의 원 에서 복소 평면에서의 반지름 1인 원에 대한 표현식이 $\cos x+i\sin x$임을 알았다. 복소평면에서 $a+bi$라고 표현하는 것에서 $a=\cos x$로 $b=\sin x$에 의해 변하면, 그 $a$와 $b$에 의해 만들어지는 점들이 원 모양을 띠는 것이다. 그리고, 여기서 $x$는 시간일 수도 있고 회전운동을 할 때의 각일 수도 있다. 

 

이 $\cos x+i\sin x$를 매클로린 전개를 해볼 것이다. 또한 04-2. 복소 지수, 자연 상수 e 에서 다뤘던 $e^{ix}$에 대해서도 매클로린 전개를 할 것이고, 끝내는 이 둘이 같음을 보일 것이다.

 

먼저, $\cos x+i\sin x$에서 $\cos x$에 대해 전개를 해보자.

 

$\cos x$에 대한 매클로린 급수 전개

 

매클로린 급수식과 계수를 구하는 (식 3)과 (식 4)를 다시 한번 써보겠다.

 

$$f(x)=\sum _{n=0}^{\mathrm{\infty }}{a}_n{x}^n(식3)$$

$$a_n=\frac{f^{(n)}(0)}{n!}(식4)$$

 

$cosx$에 대한 매크롤린 급수의 계수를 구하기 위해서는, (식 4)에서와 같이 $\cos x$에 대한 1차, 2차, ... 미분값이 필요하다. 미분을 해보자. 어떤 규칙이 있을 것이다.

 

사인/코사인 함수에 대한 미분 공식은 다음과 같다. $(\sin x{)}^{\prime }=\cos x$ $(\cos x{)}^{\prime }=-\sin x$

 

  $f(x)=\cos x$

  $f^{\prime }(x)=-\sin x$

  $f^{″}(x)=-\cos x$

  $f^{‴}(x)=\sin x$

  $f^{(4)}(x)=\cos x$   : 다시 $\cos x$로 돌아왔다.      

  $f^{(5)}(x)=-\sin x$

 

미분을 해보면, 4차 미분했을 때 원래의 $\cos x$로 돌아옴을 알 수 있다. 따라서 미분을 계속하면, 4개를 한 뭉치로 해서 반복될 것이다. 한 뭉치를 사인 함수의 첫 글자만으로 표현하면,

  $$\{c,-s,-c,s\}$$

 

이제 각 미분 값에 $x=0$를 집어넣어보면, $\{1,0,-1,0\}$이 반복된다.

  $f(0)=\cos 0=1$

  $f^{\prime }(0)=-\sin 0=0$

  $f^{″}(0)=-\cos 0=-1$

  $f^{‴}(0)=\sin 0=0$

  $f^{(4)}(0)=\cos 0=1$   

  $f^{(5)}(0)=-\sin 0=0$

 

이제 $\cos x$에 대한 매클로린 급수의 계수 값을 적어볼건데, 식으로 쭈욱 써서 표현하면 복잡하기에, 표를 이용해서 표현해 보자. 

 

	$a_0$	$a_1$	$a_2$	$a_3$	$a_4$	$a_5$	$a_6$
$f^{(n)}(0)$	$1$	$0$	$-1$	$0$	$1$	$0$	$-1$
$\frac{1}{n!}$	$\frac{1}{0!}$	$\frac{1}{1!}$	$\frac{1}{2!}$	$\frac{1}{3!}$	$\frac{1}{4!}$	$\frac{1}{5!}$	$\frac{1}{6!}$
$\cos x$	$1\cdot \frac{1}{0!}$	$0$	$-1\cdot \frac{1}{2!}$	$0$	$1\cdot \frac{1}{4!}$	$0$	$-1\cdot \frac{1}{6!}$

 

좀 복잡하긴 해도 자세히 보면 뭔가 규칙성을 보임을 알 수 있다. 

 

홀수 계수에 대해서는 모두 0의 값을 가지고, 짝수 계수에 대해서 (1,-1)이 번갈아가면서 나오고, 해당 계수의 $\frac{1}{n!}$이 곱해지는 형태이다. 

 

매클로린 급수 형태로 적어 보면,

 

$$\cos x=1+0-\frac{1}{2}{x}^2+0+\frac{1}{4!}{x}^4+0-\frac{1}{6!}{x}^6+0+\frac{1}{8!}{x}^8-\cdots$$

 

 

이제 $\sin x$에 대해서도 매클로린 전개를 해보자. 

 

$\sin x$에 대한 매클로린 전개

위의 $\cos x$에서와 똑같은 방법으로 매클로린 계수를 구해보자. 

 

먼저 $f^{(n)}(0)$ 값을 구해보자.

 

  $f(x)=\sin x$

  $f^{\prime }(x)=\cos x$

  $f^{″}(x)=-\sin x$

  $f^{‴}(x)=-\cos x$

  $f^{(4)}(x)=\sin x$   : 다시 $\sin x$로 돌아왔다.      

  $f^{(5)}(x)=\cos x$

 

미분을 해보면, 4차 미분했을 때 원래의 $\sin x$로 돌아옴을 알 수 있다. 따라서 미분을 계속하면, 4개를 한 뭉치로 해서 반복될 것이다. 한 뭉치를 사인 함수의 첫 글자만으로 표현하면,

  $$\{s,c,-s,-c\}$$

 

이제 각 미분 값에 $x=0$를 집어넣어보면, $\{0,1,0,-1\}$이 반복된다.

  $f(0)=\sin 0=0$

  $f^{\prime }(0)=\cos 0=1$

  $f^{″}(0)=-\sin 0=0$

  $f^{‴}(0)=-\cos 0=-1$

  $f^{(4)}(0)=\sin 0=0$   

  $f^{(5)}(0)=\cos 0=1$

 

$\sin x$에 대한 매클로린 급수의 계수 값을, 표를 이용해서 표현해 보자. 

 

	$a_0$	$a_1$	$a_2$	$a_3$	$a_4$	$a_5$	$a_6$
$f^{(n)}(0)$	$0$	$1$	$0$	$-1$	$0$	$1$	$0$
$\frac{1}{n!}$	$\frac{1}{0!}$	$\frac{1}{1!}$	$\frac{1}{2!}$	$\frac{1}{3!}$	$\frac{1}{4!}$	$\frac{1}{5!}$	$\frac{1}{6!}$
$\sin x$	$0$	$1\cdot \frac{1}{1!}$	$0$	$-1\cdot \frac{1}{3!}$	$0$	$1\cdot \frac{1}{5!}$	$0$

 

규칙성이 있다.

 

짝수 계수에 대해서는 모두 0의 값을 가지고, 홀수 계수에 대해서 (1,-1)이 번갈아가면서 나오고, 해당 계수의 $\frac{1}{n!}$이 곱해지는 형태이다.  (위의 $\cos x$의 경우는 짝수 값이 있고 홀수 값이 모두 0이었다. )

 

매클로린 급수 형태로 적어 보면,

 

$$\sin x=0+x+0-\frac{1}{3!}{x}^3+0+\frac{1}{5!}{x}^5+0-\frac{1}{7!}{x}^7+...$$

 

$\cos x+i\sin x$에 대한 매클로린 전개

$\cos x$와 $\sin x$의 매클로린 전개 값을 이용해서, 최종으로 우리가 구하려고 했던 $\cos x+i\sin x$에 대한 매클로린 전개를 구해보자.

 

식이 복잡하기에 표를 이용한다. ($\sin x$가 아니고 $i\sin x$를 이용했음에 유의)

 

	$a_0$	$a_1$	$a_2$	$a_3$	$a_4$	$a_5$	$a_6$
$\cos x$	$1\cdot \frac{1}{0!}$	$0$	$-1\cdot \frac{1}{2!}$	$0$	$1\cdot \frac{1}{4!}$	$0$	$-1\cdot \frac{1}{6!}$
$i\sin x$	$0$	$i\cdot \frac{1}{1!}$	$0$	$-i\cdot \frac{1}{3!}$	$0$	$i\cdot \frac{1}{5!}$	$0$
$\cos x+i\sin x$	$1\cdot \frac{1}{0!}$	$i\cdot \frac{1}{1!}$	$-1\cdot \frac{1}{2!}$	$-i\cdot \frac{1}{3!}$	$1\cdot \frac{1}{4!}$	$i\cdot \frac{1}{5!}$	$-1\cdot \frac{1}{6!}$

 

짝수 항은 $\cos x$의 값이, 홀수 항은 $i\sin x$의 값이 이용되는 형태로 식이 구성된다. 그 결과 $(1,i,-1,-i)$의 형태의 값에 $\frac{1}{n!}$ 값이 곱해지는 형태의 식이 생성된다. 

 

이러한 $1,i,-1,-i$와 같은 반복을 어디선가 본 듯하지 않은가? 

 

앞 장에서 복소지수함수 $e^{ix}$를 미분할 때, 이런 비슷한 규칙성을 본 바 있다.

 

    1차 미분: $i^1{e}^{ix}=i{e}^{ix}$

    2차 미분: $i^2{e}^{ix}=-e^{ix}$

    3차 미분: $i^3{e}^{ix}=-i{e}^{ix}$

    4차 미분: $i^4{e}^{ix}=e^{ix}$

 

    5차 미분: $i^5{e}^{ix}=i{e}^{ix}$

    6차 미분: $i^6{e}^{ix}=-e^{ix}$

    7차 미분: $i^7{e}^{ix}=-i{e}^{ix}$

    8차 미분: $i^8{e}^{ix}=e^{ix}$

    ...

 

그렇다면 $cosx+i\sin x$와 $e^{ix}$ 사이에 어떤 연관성이 있지 않을까?

 

$e^{ix}$를 매클로린 전개를 해서, 어떤 관련이 있는지 알아보자.

 

$e^{ix}$에 대한 매클로린 전개

$e^{ix}$에 대해 미분을 하고, 계수를 구해보자.

 

    $f(x)=e^{ix}$

 

    $f(0)=e^{i\cdot 0}=1$

    $f^{\prime }(0)=i\cdot e^{i\cdot 0}=i$

    $f^{″}(0)=-1\cdot e^{i\cdot 0}=-1$

    $f^{‴}(0)=-i\cdot e^{i\cdot 0}=-i$

    $f^{(4)}(0)=1\cdot e^{i\cdot 0}=1$

 

    $a_0=f(0)=1$

    $a_1=f^{\prime }(0)/1!=i\cdot \frac{1}{1!}$

    $a_2=f^{″}(0)/2!=-1\cdot \frac{1}{2!}$

    $a_3=f^{‴}(0)/3!=-i\cdot \frac{1}{3!}$

    $a_4=f^{(4)}(0)/4!=1\cdot \frac{1}{4!}$

 

$e^{ix}$에 대한 매클로린 계수와 $\cos x+i\sin x$의 매클로린 계수가 똑같다. 즉, 두 식의 매클로린 식이 똑같고, 결구 두 식은 똑같은 표현이라는 것을 알 수 있다.

 

$$e^{ix}=\cos x+i\sin x$$

 

이것이 오일러 공식이다. 

---

오일러 공식의 이해

 

오일러 공식은 수학적으로 가장 아름다운 공식으로도 불린다. 왜냐하면 이 공식이 나오기 전까지는 실수와 허수가 같이  계산되거나 하는 것이 아닌 별도의 수였고(복소수의 계산을 할 때를 생각해보라. 실수부는 실수부끼리, 허수부는 허수부끼리 더하거나 빼는 것이지, 실수부와 허수부를 더하거나 빼는 것은 없다.), 사인 함수와 지수함수는 서로 만나는 일이 없는 각자의 목적을 가진 다른 분야였다. 삼각함수는 도형의 각도를 알아내거나 원주율을 계산하거나 하는 영역, 지수와 지수함수는 그 함수로서의 계산에만 관련된 것이지, 삼각함수가 지수함수로 변환되거나 하는 것은 아니었다.  

 

이러던 것이, 이 오일러 공식에 의해, 실수와 허수가 복소평면에서 표현이 되고, 그것이 다시 사인 함수로 표현될 수 있다는 것이 알려진 것이다.

 

---

오일러 공식을 복소평면에 표현하면 다음과 같다. 

 

 

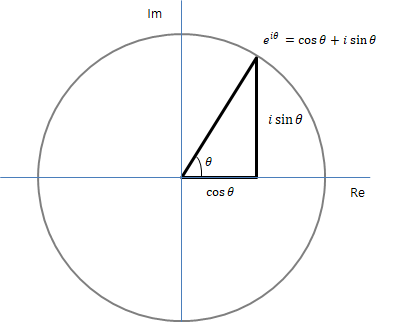
여기서 $x$ 대신에 $\theta$를 사용했다. 각도를 나타낼 때는 $\theta$를 사용하는 것이 일반적이기에 그렇게 한 것이고, 어떠한 문자를 사용해도 오일러 공식을 표현하는 데는 관계없다. 

 

복소평면에서 원을 그리는 식은 $\cos \theta +i\sin \theta$라는 것은 이미 04-1. 복소 평면, 복소평면에서의 원에서 알아본 바 있다.  이제 이것을 $e^{i\theta }$로도 표현할 수 있음을 알게 되었다.

 

---

다음 장에서는 드디어, 지금까지 4장에서 살펴본 e와 i, 그리고 오일러 공식을 이용해서 푸리에 급수의 복소표현을 알아볼 것이다. 

 

-끝-

 

 

이전글: 04-2. 복소 지수, 자연 상수 e

다음글: 04-4 푸리에 급수를 복소지수로 표현하기

다음다음글: 04-5 푸리에 급수의 삼각함수 표현 vs. 복소지수 표현