1. 알고리즘 설명
일반적으로 가장 많이 사용되는 정렬 방법이다. 지금까지 살펴봤던 정렬방법이(선택, 삽입, 거품) O(n2)의 성능을 보임에 반해, 퀵 정렬은 O(nlogn)의 성능을 보인다. ( O(nlogn) 성능을 보이는 정렬 방법으로는 퀵 정렬, 힙 정렬, 병합 정렬이 있다.)
알고리즘은 꽤 간단하다. (처음 접할 때는 생소해서 어려울 수도 있으나, 좀 익숙해지면 꽤나 직관적이라는 것을 느끼게 된다.)
기본 아이디어는 이렇다.
1. 어떤 기준점 p를 중심으로해서 왼 편에는 p보다 작은 값을, 오른 편은 큰 값이 되게한다.
2. 왼편 블록에 대해서 1번과 같은 작업을 진행 --> 재귀 호출
3. 오른편 블록에 대해서 1번과 같은 작업을 진행 --> 재귀 호출
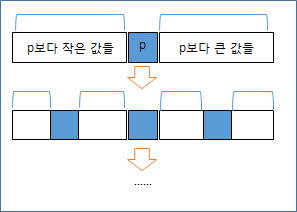
아래 애니메이션은 데이터의 가운데 값을 기준값으로 해서 퀵 정렬을 하는 모습니다.
(출처: http://www.algolist.net/Algorithms/Sorting/Quicksort )
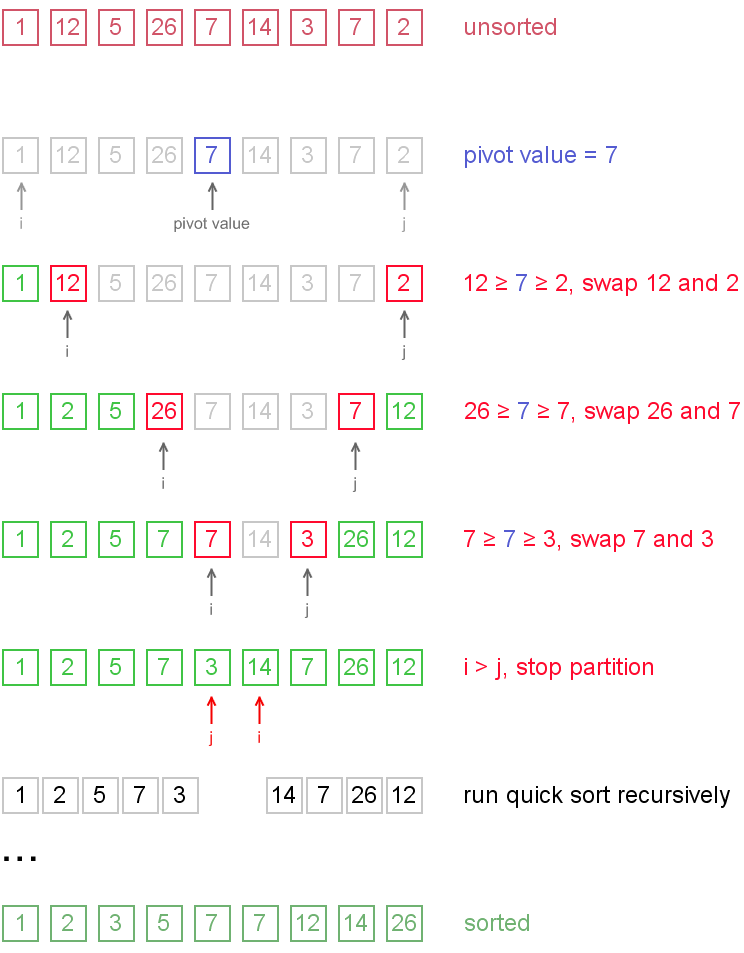
아이디어는 간단한데, 이것을 잘 구현하는 것은 좀 까다롭고 기준값을 어디로 잡느냐에 따라 여러 가지 방안이 있다. 여기서는 위 그림과 같이, 중앙을 기준값으로 잡아서 partition 진행하는 방법을 사용한다. (이 방법이 간단하면서도 효율이 좋다.)
아래 알고리즘 Flow와 소스코드를 잘 보도록 하자.
2. 알고리즘 Flow
quickSort(v,s,e) //v 데이터의 start부터 end까지를 정렬
1. if(s<e)인 경우만 실행
2. pivot = 데이터의 정중앙에 있는 값
3. i=start, j=end
4. while(i<=j)
4.1 왼쪽편 대상으로 pivot보다 큰 값이 나올 때까지 i++
4.2 오른편 대상으로 pivot보다 작은 값이 나올 때까지 j--
4.3 if(i<=j) then swap(v[i],v[j]), i++, j++
5. 왼쪽편 [s,j]에 대해 정렬(재귀 호출)
6. 오른편 [i,e]에 대해 정렬(재귀 호출)1. if(s<e) : 이 경우만 실행하고, 아닌 경우인 (s>=e)는 그냥 리턴하게 해야 한다.
이렇게 하지 않으면 재귀 호출에 의해 (s>=e)인 경우도 실행되는 에러가 발생한다.
2. pivot= 데이터의 중앙에 있는 값. 전체 데이터의 중앙값이 아니고, 위치가 중앙인 값이다.
알고리즘을 구현한 다른 소스들을 보면,
가장 첫 번째 값을 선정하거나, 가장 마지막 값을 선정하거나 해서 설명하는 게 많다.
근데, 중앙값을 선정하는 게 가장 나은 거 같다.
이유는 2가지인데, 가장 끝단으로 선정했을 경우 i++s나 j--의 처리를 잘못하면,
out of index 에러가 나올 수 있어서 코딩에 주의해야 하고, 속도 면에서도 좀 더 낫다.
3. while(i<=j)
i는 왼편 처음에서 오른 편으로 증가하는 인덱스, j는 end에서 시작해서 왼편으로 감소하는 인덱스.
이 두 개의 인덱스가 교차하기 전까지만 수행한다.
i<j의 경우뿐 아니라 i==j의 경우도 수행한다는 것에 유의
4.1 왼 편 대상으로 pivot보다 큰 값이 나올 때까지 i++
pivot 기준으로 왼쪽은 pivot보다 작은 값이 위치해야 한다.
따라서 큰 값이 나오면 교체해야 하는데, 그 큰 값이 나올 때까지 인덱스 i를 증가시키는 것이다.
4.2 오른편 대상으로 pivot보다 작은 값이 나올 때까지 j--
마찬가지로, 오른 편은 pivot보다 큰 값이 위치해야 한다.
따라서 pivot보다 작은 값이 나올 때까지 j를 이동시키는 것이고, 왼 편으로 이동하는 것이기에 j--
4.3 위 4.1과 4.2를 수행한 결과, i에는 pivot보다 큰 값이, j에는 pivot보다 작은 값이 위치해 있는데,
이때 항상 교체하는 것이 아니라 (i<=j)의 경우만 교체하고 ++i, --j를 해준다.
(i==j의 경우는 사실 교체 의미가 없다. 근데, i==j의 경우도 ++i, --j를 해줘야 하기에,
같은 조건식을 쓰기 위해서 i<=j의 한 가지 경우로 표현한 것임)
5. 왼쪽 정렬, 6. 오른쪽 정렬
기준점을 중심으로 i와 j가 교차되어 진행되었을 것이고,
그렇다면 왼 편은 \[s, j\]까지 오른 편은 \[i, e\]까지에 대해 다시 정렬을 하면 되는 것이다.이렇게 Flow를 봐도 이해가 잘 안될 수 있다. 아래 예 2개에 대해서 알고리즘 대로 손으로 풀어보면 이해하는데 도움이 된다.
{5, 2, 3, 1, 4}를 정렬하는 경우,
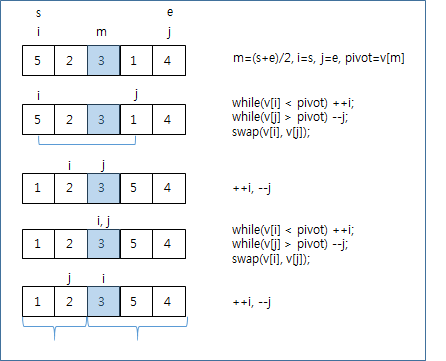
{5,2,1,3,4}를 정렬하는 경우 (중앙에 위치한 값이 제일 작은 값인 경우)
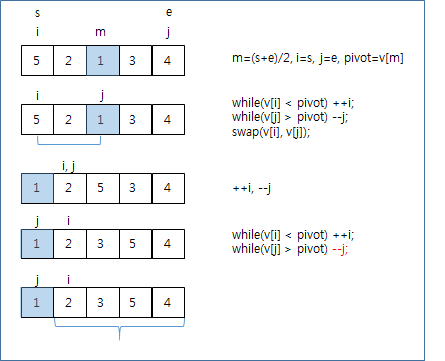
3. 소스 코드
void quickSort_normal(vector<int> &v, int s, int e){
if(s>=e) return;
int pivot = v[(s+e)/2];
int i=s, j=e;
while(i<=j){
while(v[i] < pivot) ++i;
while(v[j] > pivot) --j;
if(i<=j) {
swap(v[i],v[j]);
++i; --j;
}
};
quickSort_normal(v,s,j); quickSort_normal(v,i,e);
}
4. 시간 복잡도: O(nlogn)
최선의 경우 O(nlogn), 평균 O(nlogn), 최악 O(n2)인데, 다음 챕터에서 다루는 것처럼 기준점을 랜덤 혹은 중윗값으로 잡는 방법을 사용한다면 최악의 경우도 O(nlogn) 정도로 되기에, 시간 복잡도를 O(nlogn)으로 한 것임
5. 공간 복잡도: O(n)
6. 데이터 안정성: 없음
(같은 값에 대해서 정렬 후 원래의 순서가 보존 안됨)
7. 알고리즘 특성
기준값을 어떻게 잡느냐에 따라 수행 속도 차이가 난다. 가장 이상적인 경우는 왼쪽과 오른쪽 수량이 똑같아지도록 기준값을 잡는 것이다. 해서, 기준값을 잘 잡는 방법으로 1) 난수에 의한 2) 중윗값에 의해 분할을 하는 개선 방법이 있다. (다음 챕터에서 다룸)
또한, 재귀 호출을 사용하기에 데이터가 매우 큰 경우 프로그램 스택이 부족하여 에러가 발생할 수 있다. 이러한 문제를 해결하기 위해 재귀 호출이 아닌 일반 stack을 이용한 코딩도 가능하다. 이렇게 하면 속도도 더 빨라진다. (이 부분도 다음 챕터에서 다룸)
실제 퀵 정렬의 구현으로 어떤 것이 적합한 지가 궁금할 것이다. 자세한 것은 다음 챕터에서 다루겠지만, 결론만 얘기하면, 1) 일반적인 퀵 정렬 구현이라면 중앙 위치 pivot에 2개 인덱스 사용하며 3개 수 중윗값을 사용한 코드를 권장한다. 2) 진짜 속도가 중시되고 스택 메모리가 부족한 경우는 재귀 호출이 아닌 stack 사용한 코드 사용 3) 1번과 비슷한 속도이면서 간단한 코드를 원한다면 1개 인덱스를 사용하면서 랜덤에 의한 pivot을 선정한 방법 권고(1개 인덱스를 사용한 경우는 중윗값에 의한 기준값 선정보다 난수에 의한 선정을 한 경우가 효율이 더 좋다.).
위 3가지 경우에 대한 소스 코드를 아래에 각각 달아놨다. 참조하기 바란다.
void quickSort_median(vector<int> &v, int s, int e){
if(s>=e) return;
int m = (s+e)/2;
if(v[s] > v[m]) swap(v[s],v[m]);
if(v[m] > v[e]) swap(v[m], v[e]);
if(v[s] > v[m]) swap(v[s], v[m]);
int pivot = v[m];
int i=s, j=e;
while(i<=j){
while(v[i] < pivot) ++i;
while(v[j] > pivot) --j;
if(i<=j) {
swap(v[i],v[j]);
++i; --j;
}
}
quickSort_median(v,s,j); quickSort_median(v,i,e);
}void quickSort_stack(vector<int> &v, int s, int e){
vector<int> st((e-s+2)*2);
int top = 0;
st[++top] = e; st[++top] = s;
while (top > 0) {
int ss = st[top--];
int ee = st[top--];
if (ss < ee) {
int m = (ss+ee)/2;
if(v[ss] > v[m]) swap(v[ss],v[m]);
if(v[m] > v[ee]) swap(v[m], v[ee]);
if(v[ss] > v[m]) swap(v[ss], v[m]);
int pivot = v[m];
int i=ss, j=ee;
while(i<=j){
while(v[i] < pivot) ++i;
while(v[j] > pivot) --j;
if(i<=j) {
swap(v[i],v[j]);
++i; --j;
}
};
if(i < ee) { st[++top] = ee; st[++top] = i;}
if(ss << j){ st[++top] = j; st[++top] = ss;}
}
}
}void quickSort_simple_random(vector<int> &v, int s, int e){
if(s>=e) return;
int p = s + rand()%(e-s+1); //[s,e] 사이 난수
swap(v[p],v[e]);
p=s;
for(int i=s;i<e;++i) if(v[i]<=v[e]) swap(v[p++],v[i]);
swap(v[p], v[e]);
quickSort(v,s,p-1); quickSort(v,p+1,e);
}위 3가지 코드 모두 훌륭한 속도를 보이며, 그 비교는 다음과 같다. (모두 이미 정렬된, 그리고 역으로 정렬된 데이터에 대해서도 속도 차이가 별로 없다.)
임의의 난수 100만 개에 대한 정렬 속도
| 정렬 방법 | 100만 개 난수에 대한 정렬 시간(ms) |
| stl | sort | 389 |
| quick_median | 129 |
| quick_random | 236 |
| quick_stack | 76 |
| quick_simple_random | 136 |
| quick_simple_median | 1053 |
'Algorithm > 정렬 탐색 뻐개기' 카테고리의 다른 글
| 007. [부록]여러 가지 퀵 정렬(Quick Sort) 구현 방법(2) (0) | 2020.05.05 |
|---|---|
| 007. [부록]여러 가지 퀵 정렬(Quick Sort) 구현 방법(1) (0) | 2020.05.05 |
| 005. 거품 정렬(Bubble Sort) (0) | 2020.05.05 |
| 004. 이진 삽입 정렬(Binary Insertion Sort) (0) | 2020.05.05 |
| 003. 삽입 정렬(Insertion Sort) (0) | 2020.05.05 |

