반응형
1. 알고리즘 설명
왼쪽에서 오른쪽으로 정렬해 나가는데, 대상이 되는 i 번째 수에 대해, 이미 정렬되어 있는 왼편의 어디에 삽입하면 되는지를 찾아서 집어넣고, i를 증가시키면서 오른편 끝까지 정렬해 나간다.
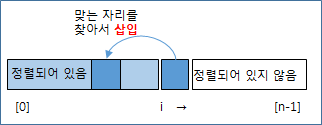
아래는 삽입 정렬이 이루어지는 에니메이션이다. (출처: wikipedia)
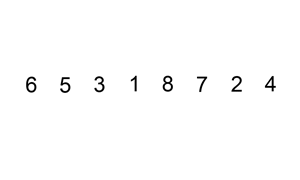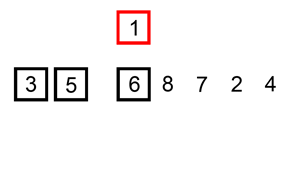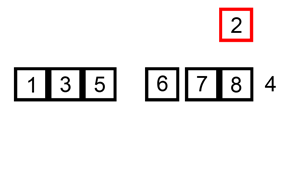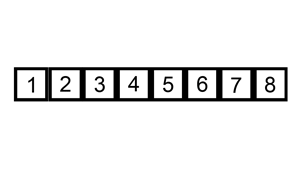
2. 알고리즘 Flow
1. i=1
2. j=i
3. j>0 이고 (v[j-1] > v[i])인 동안
3.1 v[j] = v[j-1] //v[i]가 들어갈 공간을 만든다. (오른쪽으로 쉬프트)
3.2 --j
4. v[j] = v[i] //만들어진 공간에 v[i]를 넣음
5. ++i하고 2로 돌아간다.
3. 소스 코드
void insertionSort(vector<int> &v){
int size = v.size();
for(int i=1;i<size;++i){
int key = v[i];
int j=i;
while(j>0 && v[j-1] > key){
v[j] = v[j-1]; //shift to right
--j;
}
v[j] = key;
}
}
4. 시간 복잡도: O(n2)
- 비교: 최대 n2/2
- 교환: 최대 n2/2
- i=1 : 비교(최소/최대 1회), 교환(최소 0, 최대 1회)
- i=2 : 비교(최소 1회, 최대 2회), 교환(최소 0, 최대 2회)
- i=3 : 비교(최소 1회, 최대 3회), 교환(최소 0 , 최대 3회)
...
- i=n-1: 비교(최소 1회, 최대 n-1회), 교환(최소 0, 최대 n-1회)
총 비교: 최소 (n-1)회, 최대 n^2/2
총 교환: 최소 0 (이미 정렬되어 있는 경우), 최대 n^2/2
5. 공간 복잡도: O(n)
주어진 데이터 공간을 이용해서 정렬하기에 공간 복잡도는 O(n)
6. 데이터 안정성
* 안정성(Stability): 정렬 후 같은 값에 대해 원래의 순서가 유지되는지)
안정적이다.
아래 그림처럼 오른쪽으로 이동하면서 삽입될 곳을 찾아서 들어가기에, 그 순서가 유지되고, 따라서, 안정적이라 할 수 있다.
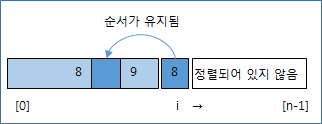
7. 알고리즘 특성
선택 선택 정렬(Selection Sort)의 경우는 많은 비교(최소, 최대 $\frac{n^2}{2}$)와 적은 교환(최소 0, 최대 n-1)이 이루어지는 데 반해, 삽입 정렬은 반대로 적은 비교와 많은 교환이 이루어진다. 또한 선택 정렬의 경우는 최선의 경우도 비교 횟수가 $\frac{n^2}{2}$이기에 $O(n^2)$인데 반해, 삽입 정렬의 경우는 최선의 경우(데이터가 이미 정렬되어 있는 경우)에는 O(n)의 성능을 보일 수 있다.
즉, 삽입 정렬의 경우는 대강 정렬되어 있는 경우에는 아주 좋은 성능을 보일 수 있기에, 퀵 정렬을 개선하는 방법으로도 사용될 수 있다. (퀵 정렬의 중간 과정에서, 퀵 정렬에 의해 어느 정도 정렬된 상태에서 삽입 정렬을 사용하면, 퀵 정렬의 단점을 개선하며 빠른 성능을 보일 수 있다.)
| 비교 | 교환 | |||
| 최소 | 최대 | 최소 | 최대 | |
| 선택 정렬 | n2/2 | n2/2 | 0 | n-1 |
| 삽입 정렬 | n-1 | n2/2 | 0 | n2/2 |
반응형
'Algorithm > 정렬 탐색 뻐개기' 카테고리의 다른 글
| 005. 거품 정렬(Bubble Sort) (0) | 2020.05.05 |
|---|---|
| 004. 이진 삽입 정렬(Binary Insertion Sort) (0) | 2020.05.05 |
| 002. 선택 정렬(Selection Sort) (0) | 2020.05.05 |
| 001. 정렬(Sorting) (0) | 2020.05.05 |
| 글쓰기에 앞서... (0) | 2020.05.05 |

