산포는 데이터의 흩어짐을 나타내는 지표로, 사분위수, 분산, 표준편차가 있다.
(최댓값, 최솟값도 산포를 나타내는 지표로 볼 수 있는데, 이 글에서는 자료를 대표하는 값으로 해서 앞 페이지에서 다뤘다. 산포로 보느냐 대푯값으로 보느냐는 관점의 차이일 뿐)
이 글에 대한 동영상 설명은,
이론 설명(1/2): youtu.be/kwEy1D3BAj8
이론 설명(2/2): youtu.be/KxigT9zega0
예제 풀이: youtu.be/McDbRHObW8I
A) 사분위수
사분위수는 데이터 값을 4개의 동일한 부분으로 나눈 값이다. 즉, 데이터를 크기순으로 배열한 후, 4개의 부분으로 나누게 되면, 첫 번째 구분되는 부분은 전체의 25%가 되는 부분(Q1)이 되고, 두 번째는 50%(Q1), 세 번 째는 75%(Q3)가 된다.
Series의 quantile 함수로 Q1, Q2, Q3 값을 구할 수 있다.
IQR(Inter Quartile Range)는 "Q3-Q1"으로, "75% 되는 지점의 값 - 25% 지점의 값"을 말한다.

구하는 예를 보면,
import pandas as pd
s = pd.Series(range(1,101)) # 1,2,...,99,100
s.quantile(0.25), s.quantile(0.75)(25.75, 75.25)
B) 분산, 표준 편차
분산은 자료들의 값이 평균과 얼마나 떨어져 있는가를 나타내는 값이다.
일견, 이를 구하기 위해서는 각 값들에서 평균과의 차를 구한 후 평균을 내면 될 것 같다. 그러나, 이렇게 하는 경우는 평균값이 항상 0이 된다.
예를 들어,
x = [2,2,3,4,4]
mean = 3
차이의 합 = (2-3)+(2-3)+(0)+(4-3)+(4-3) = -1 + -1 + 0 + 1 + 1 = 0
위와 같이 차이의 합이 항상 0이 되기에, 이러한 방법으로는 자료들이 얼마나 평균과 떨어져 있는가를 나타내는 유의미한 값을 낼 수 없다.
생각할 수 있는 방법은 1) 차이의 절댓값을 이용하는 것 2) 차이의 제곱을 이용하는 것이 있겠다.
절댓값은 이용하지 않는 게 좋다. 왜냐하면 절댓값 함수의 경우는 음수와 양수의 경계가 되는 지점에서 '불연속'이기에, 해당 함수에 대해 미분이 불가하다. 해서, 나중에 이 함숫값(분산 값)을 이용해서 미분을 해야 하는 경우에 문제가 발생하기에, 절댓값을 이용해서 분산을 구하는 것으로 정의하는 것은 좋지 않은 방법이다.
그래서, 분산을 구할 때는 '차이의 제곱'을 이용한다. (이게 분산을 구하는 방법이고, 왜 분산을 구할 때 차이의 제곱을 이용하는지에 대한 이유이다.)
모집단에 대한 분산은, '차이의 제곱'을 모두 더한 후 개수로 나눈다. 그런데, 표본집단에 대한 분산은 '차이의 제곱'을 모두 더한 후 (표본의 개수 - 1)로 나눈다. 이는 표본 집단의 분산을 '표본의 개수'로 나누는 방법으로 구하면, 원래의 모집단에 대한 분산과 오차가 커지기 때문에, 이를 보정하기 위한 방법이다.

| 정확한 설명은, 표본 분산에 대한 기댓값을 구해보면, 보분산의 (n-1)/n 배에 수렴하기에, 표본 분산으로 모 분산을 추정하기 위해서는 표본 분산에 n/(n-1)을 곱해줘서 보정해 주는 것 |
예를 들어, 아래와 같이 데이터가 있고, 이에 대한 분산을 구한다고 생각해 보자.
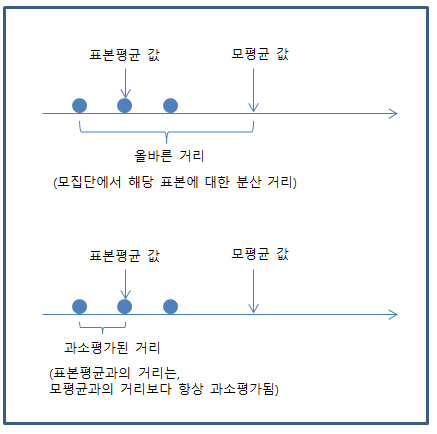
위 그림에서 보면, 원래의 모평균을 기준으로 했을 때의 차이보다, (아래 그림에서) 표본 평균을 기준으로 했을 때의 차이가 더 작다.
표본집단에 대한 값을 구하는 것은, 모집단의 값을 유추하기 위함이다. 따라서, 표본 집단에서 구하는 값이 조금이라도 모집단의 값과 유사하도록 해야 한다. 위의 그림에서 보듯이, 분산을 구할 때 표본 평균을 기준으로 할 수밖에 없는데(왜냐면 모평균을 알 수는 없으니), 표본 평균을 기준으로 분산을 구해보면 원래의 모 분산보다 작아지는 경향이 발생한다. 따라서 이 값이 커지는 방향으로 보정해야 한다. 해서, 표본의 수 n이 아니라 (n-1)로 나눠주는 것이다. (더 작은 값으로 나눠주니, 전체 값은 커지는 것)
| 위에서도 얘기했지만, 이러한 이유로 n-1로 나누는 것은 아니지만, 이렇게 이해하는 것이 이해하는데는 더 좋다. 핵심은, 표본 분산은 원래의 모분산 대비 과소평가될 수 있기에, 모분산을 구하듯이 하는 것이 아니라 (n-1)로 나눠 주는 것. |
Pandas에서 분산을 구할 때는 `var` 함수를 사용한다.
모 분산을 구할 때는 `var(ddof=0)`으로 하면 된다. 여기서 ddof는 'delta degrees of freedom'으로 '자유도'로 해석된다.
ddof=0이면 개수 N으로 나누는 것이고, ddof=1이면 (N-1)로 나누는 것이다.
표준 분산을 구할 때는 `var()` 혹은 `var(ddof=1)`로 하면 된다.
분산을 구하는 예를 보자.
s = pd.Series(range(1,101)) # 1,2,...,99,100
s.var(ddof=0) #모분산833.25
import numpy as np
np.random.seed(2)
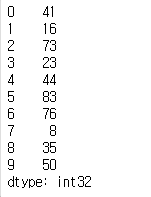
arr = np.random.randint(1,100,10)
s1 = pd.Series(arr)
s1
s1.mean()44.9
s1.var(ddof=0), s1.var(ddof=1)(602.49, 669.4333333333333)
s1.var(), s1.std()(669.4333333333333, 25.87340977400028)
v1=[] # 모분산처럼 계산 ddof=0
v2=[] # 표본분산처럼 계산 ddof=1
for i in range(1000):
s = np.random.randint(1,100,10)
v1.append(s.var(ddof=0))
v2.append(s.var(ddof=1))
np.mean(v1), np.mean(v2) (729.3544199999999, 810.3937999999999)
pd.Series(v1).mean()729.3544199999999
표준 편차(Standard Deviation)
표준 편차는 분산의 제곱근이다.
원래 분산의 의미가, 자료들 값이 평균에 얼마나 떨어져 있는가를 나타내는 지표인데, 이를 구하기 위해서 $ (값 - 평균) ^ 2$을 했었다. 해서, 이 제곱으로 되어 있는 값을 원래의 자료 값이 가지는 정도로 맞추기 위해서는 제곱근을 취하는 것이고, 이 값을 표준 편차라 하는 것이다.

Series에서 표준편차를 구할 때는 `std` 함수를 사용한다.
| Pandas에서는 대부분 표본 집단에 대한 값을 구하는 것이 디폴트이다. 분산 및 표준 편차를 구할 때도 디폴트는 표준 집단에 대한 분산, 표준 편차이다. 이는, 우리가 대하게 되는 데이터는 대부분 모집단이 아니고 표본 집단이기 때문이다. |
표준 편차를 구하는 예를 보자.
s = pd.Series(range(1,101)) # 1,2,...,99,100
s.var(ddof=0) #모분산833.25
s.std(ddof=0)23.260266550493352
np.sqrt(s.var(ddof=0))23.260266550493352
#표본 표준편차
s.std(ddof=1)24.51847376072898
C) 공분산, 상관 계수
공분산과 상관계수는, 2개의 연속형 변수의 관계성을 확인하는 통계량이다.
관계성이란, 한쪽 변수의 값이 커지거나 작아질 때 나머지 변수의 값이 어떻게 변하느냐 하는 관계성을 말한다.
예를 들어, 변수 x는 키를 나타내고, 변수 y는 몸무게를 나타내고, 만약 키가 커짐에 따라 몸무게가 크다면, 두 변수는 "양의 상관성"이 있다고 할 수 있고, 키가 커짐에 따라 몸무게가 작아진다면 "음의 상관성"이 있다고 할 수 있다.

공분산을 구하는 식을 보면 "x의 평균값과의 차이"와 "y의 평균값과의 차이"를 곱한 것에 대한 평균값이다. (전부 더한 후 개수로 나눴으니, 평균인 셈)
이는, 분산을 구할 때 "평균과의 차이"와 "평균과의 차이"를 곱한 것과 유사하다. (제곱이니깐 따로따로 곱한 것과 같다.)
그래서 "공분산"이라고 한다.
그런데, 왜 각 변수의 차이를 곱한 것의 평균을 하면, 두 변수의 관계성을 알 수 있게 되는 것일까?
아래 그림을 보자.

왼쪽 그림을 보면, 두 점을 이으면 우상향의 직선이 될 것이다. 기울기가 양수인 직선, 즉 x가 커지면 y가 커지는 관계성을 보인다. 실제로 $(x_1, y_1)$에 대해서 평균과의 차이를 구한 후 곱을 해보면 $(x_1-\mu_1)(y_1-\mu_1)>0$이 됨을 알 수 있다. 마찬가지로 $(x_2, y_2)$에 대해서도 구해보면 $(x_2-\mu_2)(y_2-\mu_2)>0$이다.
즉, $cov(X, Y)>0$이고, 이 대 두 변수의 관계는 양의 상관성을 가진다.
오른쪽 그림을 보면, 두 점을 이으면 우하단의 직선이 된다. 기울기가 음수인 직선.
여기서 $(x_1-\mu_1)(y_1-\mu_1)<0$ 이고 $(x_2-\mu_2)(y_2-\mu_2)<0$이다.
즉, $cov(X, Y)<0 $이고, 이 때 두 변수의 관계는 음의 상관성을 가진다.
Pandas에서 공분산은cov 함수로 구할 수 있다
분산을 구할 때와 마찬가지로, 모집단인 경우와 표본집단의 경우에 대해서, 개수 N으로 나누는지 (N-1)로 나누는지의 차이가 있고, 함수를 사용할 때는 ddof값을 지정해서 구한다. 모집단에 대해서만 ddof=0으로 지정하면 된다.
표본에 대한 공분산: s1.cov(s2) df.cov()
모집단에 대한 공분산: s1.cov(s2,ddof=0) df.cov(ddof=0)
공분산 풀이 예를 보자.
from sklearn.datasets import load_iris
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df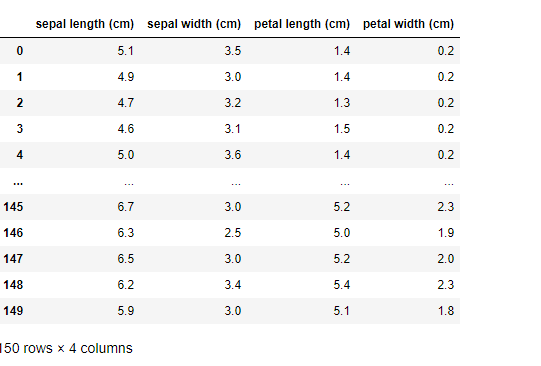
iris(붓꽃)의 꽃받침(petal)의 길이와 너비, 꽃잎(sepal)의 길이와 너비에 대한 데이터이다.
df['sepal length (cm)'].cov(df['sepal width (cm)'])-0.04243400447427291
df['sepal length (cm)'].cov(df['petal length (cm)'])1.2743154362416111
df.cov()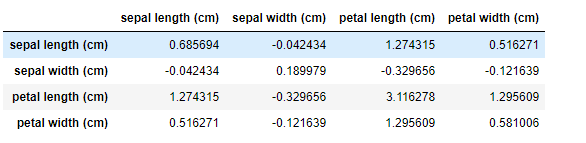
상관계수 (Correlation)
상관계수는 공분산의 값이 [-1,1] 사잇값이 되게 조정한 값이다. 공분산에 대해 표준화를 했다고 볼 수 있는데, 공분산이 단위 척도에 따라서 값이 커지고 작아지고 하는데 반해, 상관계수는 모든 값을 [-1,1] 사이로 표준화했기에, 단위가 다른 변수들에 대한 비교도 가능하다.
예를 들어, 하나는 [1000, 10000] 사잇값에 대한 두 변수의 공분산이고, 다른 하나는 [1,10] 사잇값에 대한 공분산이면, 두 공분산에 대해 어느 것이 더 큰 값인지를 판단하기가 쉽지 않다. 첫 번째 공분산 값이 무조건 클 텐데, 그렇다고 해서 첫 번째 사례의 값들이 더 큰 상관관계를 가지고 있다고 할 수 없는 것이다. (단위가 커서 크게 보일 뿐)
그러나, 이를 상관계수로 나타내면 두 값과의 대소관계에 의해서, 상관관계가 크다/작다를 얘기할 수 있다. 값을 [-1,1] 사잇값으로 변환했기 때문.

상관계수의 계산은 corr 함수를 사용하면 된다.

일반적인 수치형 값들의 경우에는 파라미터 없이 corr()을 쓰면되고, 이렇게 하면 피어슨 상관계수를 구하는 것이다. (위 쪽에 나온 수식이 피어슨 상관계수를 구하는 수식)
그런데, 값들이 순위를 나타내는 값이면 계산식이 달라진다. (여기서 소개는 안 하겠다.) 이럴 때도 상관계수를 구할 수 있는데(한쪽 순위가 높아질 때 다른 쪽 순위가 어떻게 되는지에 대한 관계를 구함), 그 방법으로는 스피어만(spearman)과 켄달(kendal)이 있다.
구하는 것은 쉽다. corr함수의 파라이터로 방법 이름을 지정하면 된다.
df.corr(method='searman')
상관계수를 구하는 예를 보자.
df['sepal length (cm)'].corr(df['sepal width (cm)'])-0.11756978413300204
df['sepal length (cm)'].corr(df['petal length (cm)'])0.8717537758865831
df.corr()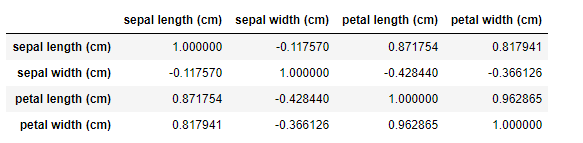
"산포: 사분위, 분산/표준편차, 공분산/상관계수"에 대한 예제
아래 예제 1.7~1.9번까지에 대해, sklearn패키지에 있는 iris 데이터를 사용하시오.
데이터 불러오기 방법:
from sklearn.datasets import load_iris
iris = load_iris()
# DataFrame으로 만들기
df = pd.DataFrame(iris.data, columns=iris.feature_names)iris 데이터에는 다음과 같은 칼럼 존재
- sepal length (cm) : 꽃 받침 길이
- sepal width (cm) : 꽃 받침 너비
- petal length (cm) : 꽃 잎 길이
- petal width (cm) : 꽃 잎 너비
sklearn 패키지가 설치되어 있지 않다면 pip install을 통해 설치
pip install sklearn
예제 1.6
iris 데이터로 구성된 df에, 각 칼럼에 대해 이상치를 제거하고자 한다.
이상치는 (Q1 - 1.5 x IQR)보다IQR) 보다 작거나, (Q3 + 1.5 x IQR) 보다 큰 값을 말한다.
- Q1: 데이터의 25% 지점의 값
- Q3: 데이터의 75% 지점의 값
- IQR: Interquartile Range
각 칼럼별로 이상치를 제거한 후, 각 칼럼의 평균을 구하시오
<풀이 전략>
- s.quantile() 사용
- IQR = Q3 - Q1
- 여러개 칼럼이기에, 이상치제거후 평균을 구하는 함수 제작
df.head(2)
def cal_mean(s):
q1 = s.quantile(0.25)
q3 = s.quantile(0.75)
iqr = q3-q1
low = q1 - 1.5*iqr
high = q3 + 1.5*iqr
c = (s>=low) & (s<=high)
return s[c].mean()
for col in df.columns:
print(col, cal_mean(df[col]))
s.describe()
예제 1.8
iris 데이터로 구성된 df에 대해, 앞 예제 1.7과 달리, 새로운 기준으로 이상치를 제거하고자 한다.
새로운 기준에 의한 이상치는 (Median - 1.5 x IQR) 보다 작거나, (Median + 1.5 x IQR) 보다 큰 값을 말한다.
- IQR: Interquartile Range
1) 각 칼럼별로 새로운 기준으로 이상치를 제거한 후 각 칼럼의 평균을 구하시오.
2) 새롭게 구한 각 칼럼 별 평균을 A라 하고, 예제 1.7에서 구한 평균을 B라 할 때, A와 B의 차의 절댓값을 구하시오
3) 차이의 절댓값이 가장 큰 칼럼을 적으시오
df.head(2)
s = df['sepal length (cm)']
def cal_mean2(s):
q1 = s.quantile(0.25)
q3 = s.quantile(0.75)
iqr = q3-q1
m = s.median()
low = m - 1.5*iqr
high = m + 1.5*iqr
c = (s>=low) & (s<=high)
return s[c].mean()
import numpy as np
for col in df.columns:
diff = cal_mean2(df[col])-cal_mean(df[col])
print(col, np.abs(diff))
s.describe()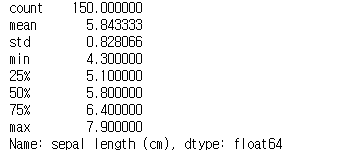
예제 1.9
iris 데이터 df에 대해서, 각 칼럼간의 양의 상관관계가 가장 큰 두 칼럼을 찾고, 그 두 칼럼의 공분산(covariance)을 구하시오. 이때, 데이터는 표본집단이라고 가정하고 공분산을 구하시오. (소수점 셋째 자리에서 반올림해서 소수점 2자리까지 구하시오)
df.corr()
df['petal length (cm)'].cov(df['petal width (cm)'])1.2956093959731545
# 답) 1.30
첨부:
-끝-
다음 글: 1.3 데이터 스케일링
'Information > 통계강의' 카테고리의 다른 글
| 1.3 데이터 스케일링 (예제 풀이) (0) | 2021.02.13 |
|---|---|
| 1.3 데이터 스케일링 (이론) (0) | 2021.02.13 |
| 1.1 대푯값 (예제 풀이) (0) | 2021.02.12 |
| 1.1 대푯값 (이론) (0) | 2021.02.12 |
| 1. 통계량 (0) | 2021.02.12 |



