이번 페이지에서는, 수학에서의 '행렬' 데이터를 처리할 수 있는 자료형인 numpy.array에 대해서 알아보겠습니다.
넘파이(NumPy)는 파이썬에서 과학/수학 계산을 할 수 있도록, 여러 가지 과학/수학용 자료형/함수들이 들어있는 라이브러리입니다. (과학자/수학자들이 파이썬으로 프로그래밍하다가, 필요한 기능들을 만들었고, 이것들을 집대성해서 일반인도 쓸 수 있게 공개한 것이 '넘파이' 라이브러리입니다.)
여기서는 넘파이의 행렬 계산 기능을 중심으로 살펴볼 것입니다.
왜 행렬이 필요한가? (왜 행렬까지 공부해야 하는가?)
파이썬의 기본 자료형인 리스트(list), 딕셔너리(dict), 튜플(tuple), 집합(set)을 공부했는데, 기본 자료형도 아닌 numpy.array라는 것을 왜 알아야 하는 걸까요?
이유는, 데이터를 다룰 때 데이터를 행렬로 표시하고 연산을 해야만 효율적일 때가 많기 때문입니다.
간단한 예로, 주식 데이터에서 일간 최고가와 최저가를 처리하는 예를 들어보겠습니다.
| A라는 주식의 영업일 5일간의 주가가 다음과 같다고 할 때, 각 날자별 최고가와 최저가 차이를 구하세요. |
| 날짜 | 최고가 | 최저가 |
| 7월 1일 | 1100 | 1000 |
| 7월 2일 | 1200 | 1000 |
| 7월 3일 | 1300 | 1200 |
| 7월 4일 | 1500 | 1450 |
| 7월 5일 | 1600 | 1300 |
최고가, 최저가를 리스트로 표현한 후 계산하는 코드는 다음과 같을 것입니다.
고가 = [1100, 1200, 1300, 1500, 1600]
저가 = [1000, 1000, 1200, 1450, 1300]
차이=[]
for i in range(0, len(고가)):
차이.append(고가[i] - 저가[i])
print(차이) # [100, 200, 100, 50, 300]위 코드를 보면 for 루프를 이용해서 '고가'와 '저가' 리스트 값들을 차례로 읽으면서, 그 차이 값을 구한 후 그것을 '차이'라는 리스트에 append 하고 있습니다.
이것을, for루프를 사용하지 않고, '차이 = 고가 - 저가'처럼 간단히 연산할 순 없을까요?
numpy.array를 이용해서 행렬로 만든 후 사용하면 가능합니다.
고가 = [1100, 1200, 1300, 1500, 1600]
저가 = [1000, 1000, 1200, 1450, 1300]
import numpy as np
고가행렬 = np.array(고가)
저가행렬 = np.array(저가)
차이행렬 = 고가행렬 - 저가행렬
print(차이행렬) #[100 200 100 50 300]
차이 = list(차이행렬)
print(차이) #[100, 200, 100, 50, 300]위 코드에 보면 '차이행렬 = 고가행렬 - 저가행렬' 처럼, 단순하게 마이너스 연산을 사용해서, 각 원소끼리의 뺄셈 연산이 가능했습니다.
이처럼 각 행렬의 각 원소끼리의 사칙연산 및 행렬곱 등을 numpy.array를 이용하면 쉽게 할 수 있고, 이러한 데이터 연산이 뒤에 배우게 되는 데이터 마이닝이나 딥러닝에 꼭 필요한 요소이기에, numpy.array에 대해서 기본적인 사항은 알아야 합니다.
1. 행렬 기본
수학에서의 행렬에 대해서 간단하게 알아보겠습니다. 기본적인 사항만.
행렬은, 수나 수식을 사각형의 배열로 나열한 것을 말합니다. 이때, 가로 줄을 행(Row), 세로 줄을 열(Column)이라고 합니다.

행렬끼리의 덧셈/뺄셈/곱셈/나눗셈
두 행렬의 대응되는 원소끼리 더하거나 빼거나 곱하거나 나누는 연산입니다. 이때 두 행렬의 행과 열의 차수가 같아야 합니다.

행렬에 대한 상수 덧셈/뺄셈/곱셈/나눗셈
행렬에 대해 어떤 상수를 더하거나/빼거나/곱하거나/나누면, 행렬의 원소 하나하나에 대해 그 상수값을 더하거나/빼거나/곱하거나/나누게 됩니다.

행렬곱
행렬의 곱은, 대응되는 원소끼리 곱하는 것이 아닙니다. 아래 그림처럼 원소들 간의 곱과 합으로 계산이 됩니다.
일반적으로 '행렬곱'이라고 하면 같은 위치에 있는 원소를 곱하는 것을 의미하지 않고, 아래 설명과 같은 방식으로의 곱을 얘기합니다.
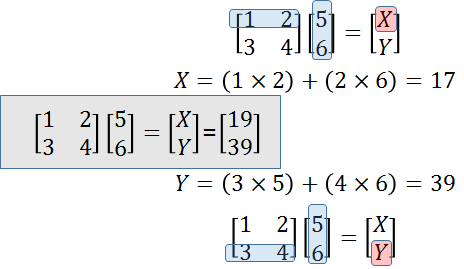
위 그림에서와 같이 행렬 곱은 왼쪽 행렬의 행과 오른쪽 행렬의 열을 원소별로 곱하고, 그 값들을 더해서 계산합니다. 그리고 그 결과가 새로운 행렬의 (행,열)의 값이 됩니다.
예제에서 왼쪽 행렬의 1번 행과 1번 열을 곱한 후 합한 것이 새로운 행렬의 (1,1) 위치의 X 값이 되었고,
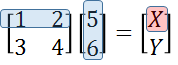
왼쪽의 2번 행과 오른쪽의 1번 열이 곱해지고 더해져서 결괏값 행렬 (2,1) 위치의 Y가 되었습니다.
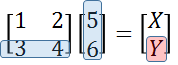
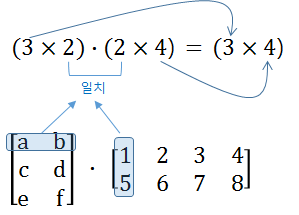
여기서 주의할 것은, 왼쪽 행렬의 각 행에 대한 원소의 개수와, 오른쪽 행렬의 각 열에 대한 원소의 개수가 같아야 한다는 것입니다. 뭐 당연히 서로 곱하고 더하기 위해서는 원소의 갯수가 같아야하는 겁니다. 즉, 아래 그림에서 파란색으로 된 박스안의 원소의 갯수가 서로 같아야한다는 것입니다.
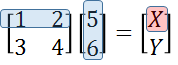
예를 들어 왼쪽이 (3 x 2) 행렬이고 오른쪽이 (2 x 4) 행렬이면, 왼쪽의 열과 오른쪽의 행의 차수가 같기에 행렬곱이 가능하고, 결과는 왼쪽의 행 차수인 3과 오른쪽 열 차수인 4에 의해 (3x4) 행렬이 됩니다.
행렬곱 계산을 어떻게 하는지 좀 더 알고 싶다면, 아래 동영상 참조하세요
2. NumPy 설치
NumPy는 파이썬 안에 기본으로 들어 있지 않습니다. 해서, 따로 설치해야 합니다.
설치는 어렵지 않습니다.
1) 윈도즈 명령어 창 연다.
"윈도 키 + R" --> "cmd" 타이핑

2) 'pip install numpy'라고 타이핑하고 Enter
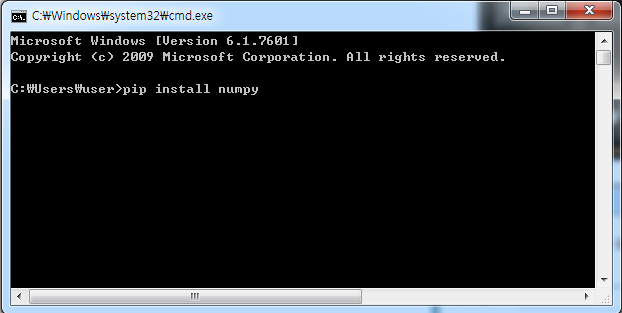
이처럼 파이썬에 필요한 외부 라이브러리는 'pip install' 명령을 통해서 쉽게 설치할 수 있습니다.
3. array 생성 및 사용
import numpy
파이썬에서 외부 라이브러리 모듈을 사용하기 위해서는, 해당 라이브러리를 이번 코드에서 사용한다는 것을 알려주는 'import <라이브러리 모듈 이름>'라는 코드에 적어줘야 합니다.
import numpy as np뒤에 'as np'는 'numpy라는 모듈 이름을 np로 축약해서 사용할게요'라는 의미입니다.
따라서, 원래 'numpy.array( )'라고 해야 할 것을 'np.array( )'라고 할 수 있는 것입니다.
파이썬에서는 이처럼 긴 단어를 가능한 짧은 단어로 해서 사용하려고 노력하는 것이 관습입니다. pandas의 경우도 'import pandas as pd'와 같이 'pd'로 단축해서 사용할 겁니다.
array의 생성
행렬로 사용될 array는 리스트 데이터를 이용해서 만들 수 있습니다.
a = np.array([1,2,3,4])
b = np.array([
[1,2],
[3,4],
])
print(b)위 코드에서 b는 (2x2) 행렬입니다. 이처럼 다차원 행렬을 만들 때는 리스트를 여러 개 사용해서 만듭니다.
[심층 해설]
넘파이의 'array( )'메서드로 만들어지는 것은 Numpy.ndarray라는 객체입니다. ndarray는 'n-dimensional array'라는 의미로 'n 차원의 배열'을 나타냅니다.
행렬은 여러 개의 배열이 모인 것이라고 할 수 있습니다. 그렇기에 넘파이에서는 n차원의 배열을 나타내는 ndarray로 행렬을 나타낼 수 있고, 이러한 ndarray를 만드는 numpy.array()가 행렬을 표현하는 데이터를 만든다고 할 수 있겠습니다.
두 행렬의 덧셈/뺄셈
두 행렬의 같은 자리에 있는 원소끼리 덧셈/뺄셈을 할 수 있습니다. (곱셈도 가능하나, 이다음에 설명하는 행렬의 곱과 혼돈될까 봐 그냥 덧셈/뺄셈만 해봅니다.)
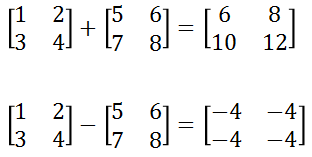
import numpy as np
a = np.array([[1,2],[3,4]])
b = np.array([[5,6],[7,8]])
합 = a + b
차 = a - b
print(합)
print(차)
두 행렬의 곱
행렬곱은 'dot' 메서드를 사용해서 합니다.
'a * b'를 하게 되면, 같은 자리에 있는 원소끼리의 곱 계산이 이루어집니다. dot 메서드를 사용해야 왼쪽의 행과 오른쪽의 열을 곱하고 더하는 '행렬곱' 연산이 이루어집니다.
import numpy as np
a = np.array([[1,2],[3,4]])
b = np.array([[5,6],[7,8]])
행렬곱 = np.dot(a,b)
print(행렬곱)
'dot' 메서드에 이루어지는 계산은 다음과 같습니다.
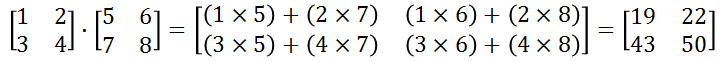
-끝-
다음글: 04-5 데이터 프레임(pandas.DataFrame)
목차로 이동: [목차]CxO를 위한 코딩 강좌(파이썬을 중심으로)
'Programming > CxO를 위한 코딩' 카테고리의 다른 글
| 04-5 데이터 프레임(pandas.DataFrame) (0) | 2020.06.29 |
|---|---|
| 04-4 집합(set) (0) | 2020.06.25 |
| 04-3 튜플(tuple) (0) | 2020.06.25 |
| 04-2 딕셔너리(dict) (0) | 2020.06.25 |
| 04-1 리스트(list) (0) | 2020.06.25 |
