시간이 흐름에 따라 점점 펄스파(구형파)처럼 변하는 애니메이션을 만들어보겠다.
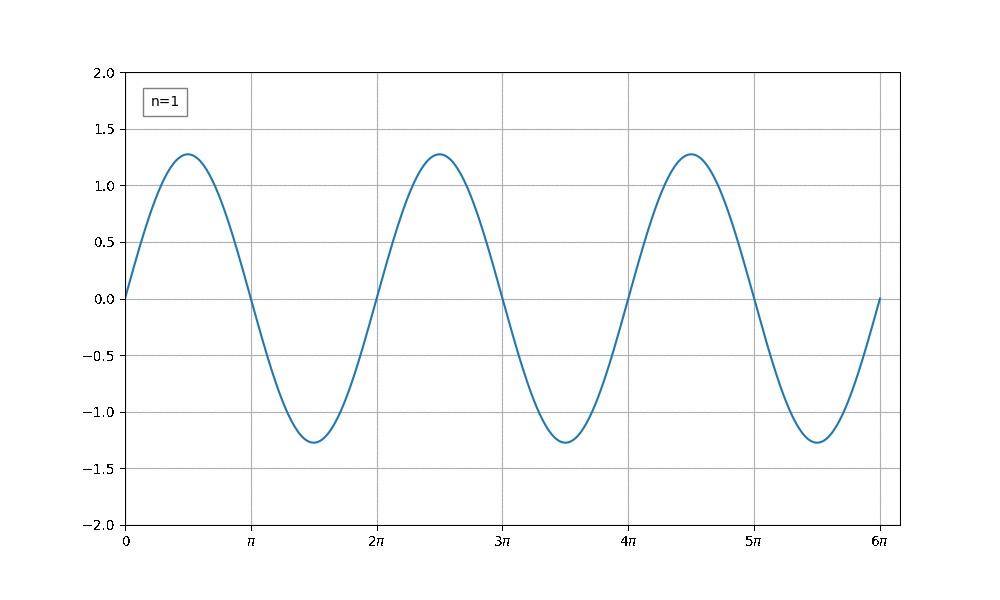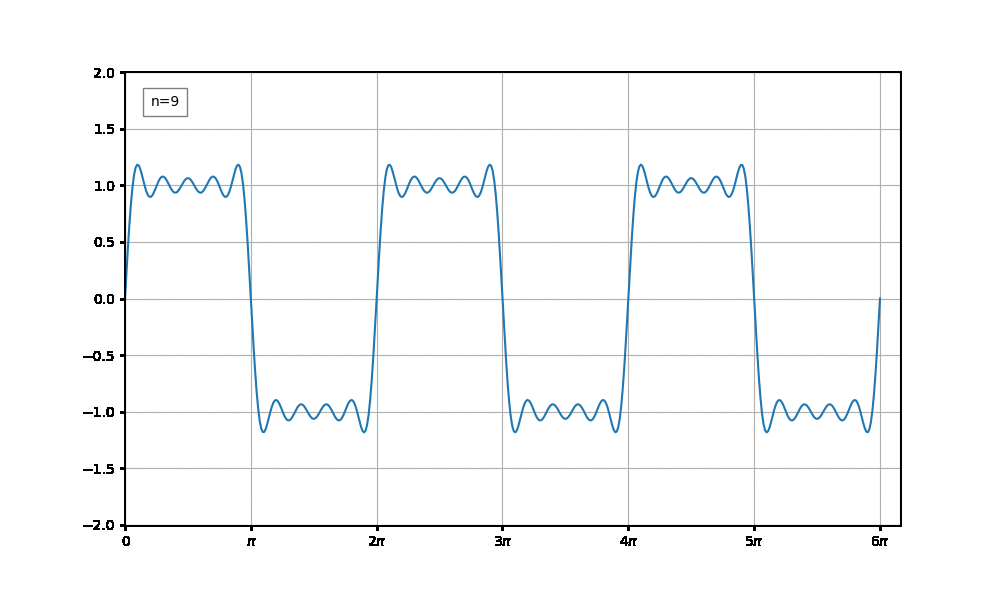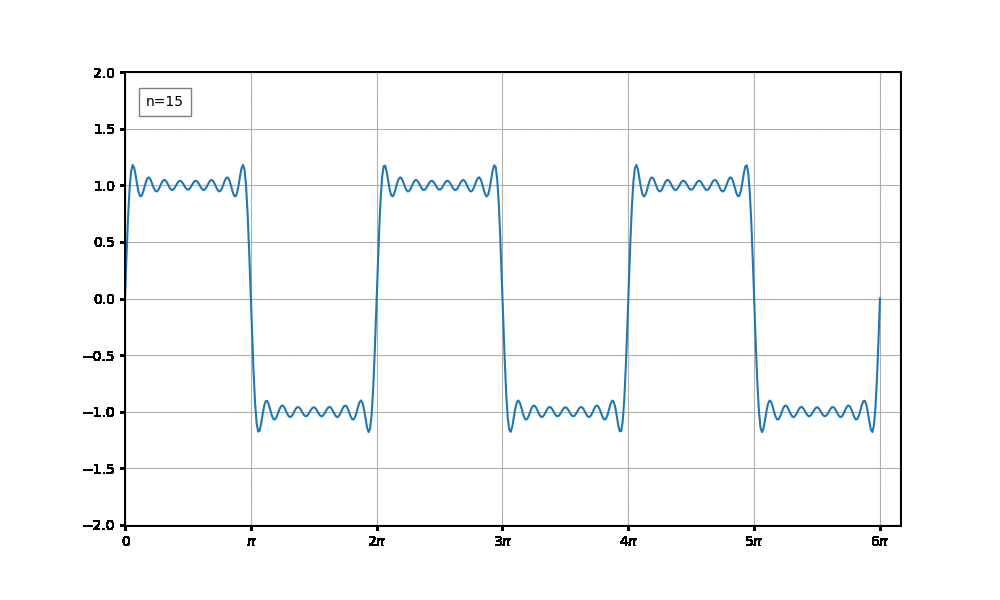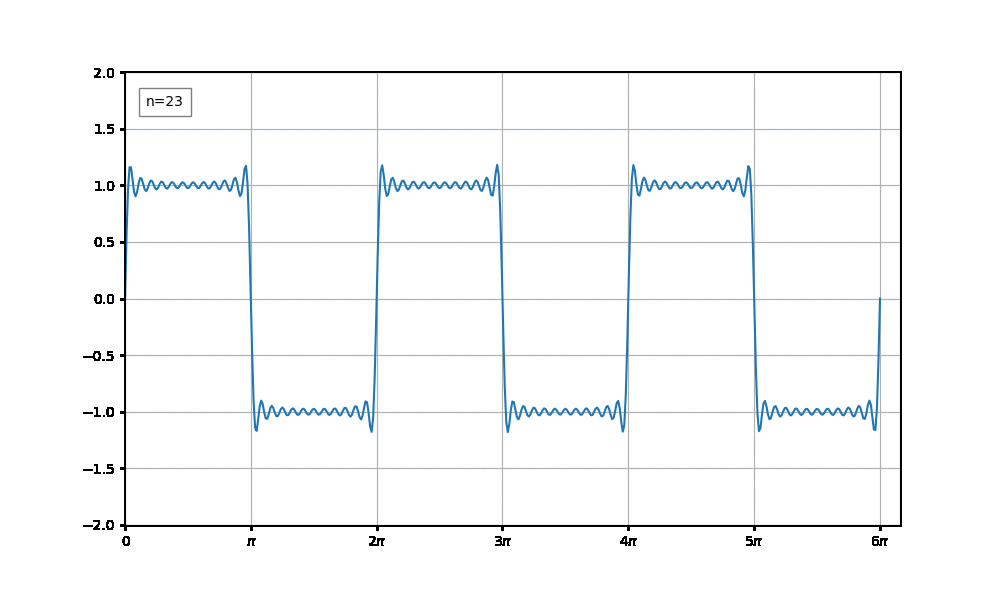
이러한 파형을 그리는 수식은 아래와 같다.
$$ \sum _{n=1} ^{\infty} {\frac {4}{n\pi} \sin {nx}}$$
이 수식은, 아래 그림과 같은 완벽한 펄스파를 푸리에 급수로 변환하면 나온다.
유도식이 궁금하면 여기 참조: 04-6. 푸리에 급수 예제를 손으로 풀어보기
이 애니메이션을 만들기 위한 핵심 코드는 아래와 같다.
title = ax.text(1,1.7,"",bbox={'facecolor':'w', 'alpha':0.5,'pad':5},ha="center")
def update(i):
global yy
y = (4/(i*np.pi))*np.sin(i*x)
yy += y
line.set_data(x, yy)
title.set_text("n="+str(i))
return line,title,
먼저 'title'에 대한 설명부터 하자면, 애니메이션에서 n=1, n=2,...처럼 n의 값이 변하는 모습을 보여주기 위한 코드이다.
유의할 점은, title을 축을 나타내는 ax에 의해 지정했다는 점.
title = ax.text(1,1.7,"",bbox={'facecolor':'w', 'alpha':0.5,'pad':5},ha="center")
def update(i):
...
title.set_text("n="+str(i))
return line,title,일반적으로 title을 지정하는 방법인 plt.title( )에 의해 지정하면, 값이 바뀌지 않는다. 왜냐하면, FuncAnimation에서 blit=True로 했기 때문에, 그래프의 정적인 요소들은 바뀌지 않을 것이고, plt.title에 의한 title은 '정적인 요소'로 간주되기 때문일 것이다.
return 값으로 line 뿐만 아니라 title값도 해줘야 한다. 그래야 변하는 요소로 간주되어 애니메이션으로 나타날 것이다.
실제 펄스파를 만드는 부분은 아래와 같은 코드.
global yy
y = (4/(i*np.pi))*np.sin(i*x)
yy += y
line.set_data(x, yy)
전달되는 $i$값은 홀수만 전달이될 것이고(FuncAnimation의 frames에다가 홀수만 전달되도록 함),
ani = FuncAnimation(fig=fig, func=update, frames=range(1,25,2),
init_func=init, interval=1000, blit=True)
$y=\frac{4}{i\cdot \pi} \sin {(ix)}$에 의해 생성된 파형들이 계속 합쳐져서 yy 값이 된다.
y = (4/(i*np.pi))*np.sin(i*x)
yy += y여기서 yy 변수를 global 처리한 것에 유의.
yy += y는 yy = yy + y와 같고, 이 함수 내에서 'yy = ... '이라고 되어 있기에 'yy'는 지역변수가 되고(파이썬에서의 변수 참조 우선순위 규칙에 의해. 지역변수가 가장 우선순위 높음. 전역 변수로 yy가 있어도 함수 내에서 다시 선언한 yy는 전역 변수인 yy가 아닌 그냥 새로운 지역변수가 됨),
그 뒤에 'yy = yy + y'라고 다시 yy가 쓰였기에, 뒤에 쓰인 yy는 지역변수 yy를 가리키는 것이 됨. 이때 이 지역변수 yy에는 아무 값도 할당되지 않은 상태이기에, yy를 global로 처리하지 않으면 에러가 뜰 것임
| 이 수식에 의해서 왜 펄스파가 될까? y가 되는 수식을 자세히 보면, - 사인파의 진폭을 나타내는 부분은 $\frac{4}{i\cdot \pi}$로, $i$가 증가할 수록 그 값이 작아진다. - 주파수에 영향을 주는 부분은 $\sin$ 함수 안에 있는 $ix$로, i값이 커질수록 커진다. 즉, 주파수가 커짐(주기는 짧아짐) 즉, i=1일 때가 기본 주파수파(가장 주기가 긴 파형=주파수가 작은 파형)이고, 이 기본 주파수를 기준으로해서, 거기에다가 진폭은 점점 작아지면서 주기가 짧은 파형들이 생성되어 더해지게 되니, 애니메이션처럼 점점 펄스파에 가까운 모습으로 변하게 되는 것이다. |
전체 코드는 아래와 같다. 헷갈릴만한 부분은 주석을 달았다.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from matplotlib import rc
fig, ax = plt.subplots(figsize=(10,6))
ax.grid()
x, y = [], []
x = np.linspace(0, 6*np.pi, 500)
yy = x*0 #x의 크기만큼 0으로 채워진 리스트를 만들 때의 전형적인 기법임
line, = plt.plot([], [], )
# ax의 text로 지정한 것에 유의
title = ax.text(1,1.7,"",bbox={'facecolor':'w', 'alpha':0.5,'pad':5},ha="center")
def init():
ax.set_xlim(0, 6*np.pi+0.5) #코드 위 쪽에서 x의 값을 6pi까지 잡아놨었다. 그 크기랑 맞춘것임
ax.set_ylim(-2.0, 2.0)
# X축 단위 표시를 pi 단위로 표시
ax.set_xticks([0,np.pi,2*np.pi,3*np.pi,4*np.pi,5*np.pi,6*np.pi])
ax.set_xticklabels(['0',r'$\pi$',r'$2\pi$',r'$3\pi$',r'$4\pi$',r'$5\pi$',r'$6\pi$'])
return line,
def update(i):
global yy
y = (4/(i*np.pi))*np.sin(i*x)
yy += y
line.set_data(x, yy)
title.set_text("n="+str(i))
return line,title,
# 25 frames x 200ms = 5초
ani = FuncAnimation(fig=fig, func=update, frames=range(1,25,2),
init_func=init, interval=1000, blit=True)
rc('animation', html='html5')
ani
-끝-
'InfoGraph > 파이썬 matplotlib 애니메이션' 카테고리의 다른 글
| [찾아보기]matplotlib로 만든 애니메이션 모음 (0) | 2021.03.27 |
|---|---|
| 03. [예제]흐르는 물결같은 사인파(사인 그래프, sine graph) 그리기 (0) | 2021.03.26 |
| 02. [예제]사인 곡선(사인 그래프, sine graph) 그리기 (0) | 2021.03.23 |
| 01. matplotlib를 이용해서 애니메이션 그래프(Animation Graph) 만들기 (0) | 2021.03.23 |



