설명에 사용된 ipynb파일은,
분포
분포(확률분포, Probability Distribution)는 확률 변수가 특정한 값을 가질 확률을 나타내는 함수를 의미한다. 그래프로 나타낸다면 가로축은 가질 수 있는 값이, 세로축은 그 값이 나올 확률로 나타낼 수 있겠고, 이때 각 값과 확률과의 관계가 분포 함수가 된다.
예를 들어, 동전을 1번 던져서 앞면이 나오는 횟수를 변수로 둔다면, 나올 수 있는 변수의 값은 0 혹은 1이다. 앞면이 안 나오거나 한 번 나오거나. 그리고 0일 확률은 50%, 1일 확률도 50%이고, 두 확률을 더하면 1이 된다.
만약, 동전을 4번 던져서 앞면이 나오는 횟수를 변수로 둔다면, 나올 수 있는 변수의 값은 {0,1,2,3,4}이고 (한 번도 안 나오면 0, 한 번 나오면 1,...) 각 변수 값에 대한 확률은 {0:0.125, 1:0.375, 2:0.5, 3:0.375, 4:0.125}이다. (계산과정은 아래 그림 참조)
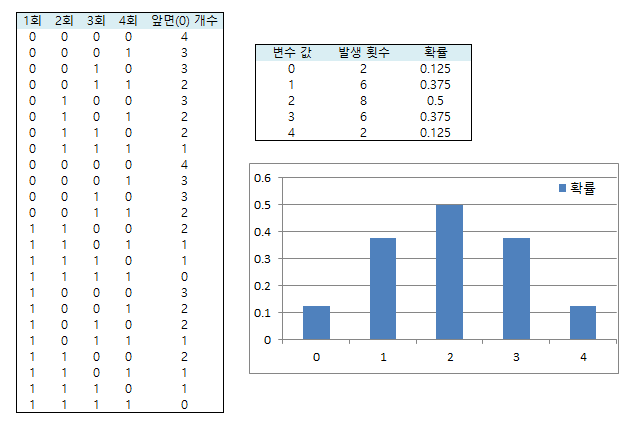
이처럼, 나올 수 있는 각 변수의 값 대비 확률 값을 표현한 것이 '분포(확률 분포)'이고, 변수와 확률 간의 관계를 수식으로 나타낸 것이 '확률 분포 함수'이다.
정규 분포
정규 분포는 평균($\mu$)과 표준편차($\sigma$)에 대해 아래와 같은 확률 분포 함수 식을 만족하는 분포이다. (데이터 분석만을 위해서는, 수식을 외울 필요 없고, 굳이 이 수식이 왜 종모양의 그래프가 되는지도 알 필요 없다. 단지 평균과 표준편차가 관련된 수식이라는 것만 알고 있으면 된다.)
$$ f(x) = \frac{1}{\sigma\sqrt{2\pi}}exp(-\frac{{(x-\mu)}^2}{2\sigma^2})$$
정규분포의 그래프 모양은,
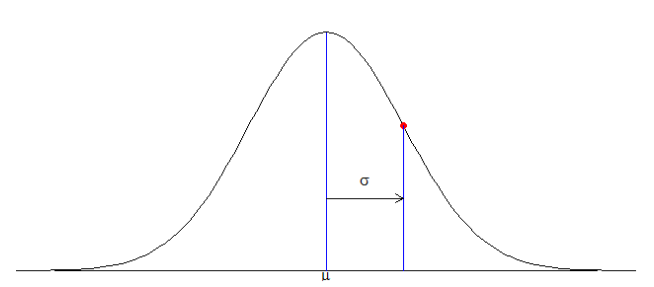
정규분포의 대표적인 성질은,
- 정규분포 곡선은 좌우 대칭. 곡선 아래 면적은 1
- 평균 == 중앙값 == 최빈값
정규분포가 중요한 이유는, 많은 현상과 자료들이 정규분포와 유사한 분포를 띄고 있기에, 그 현상에서 특정 사건이 일어날 확률(=어떤 값에 대한 확률)을 정규분포 함수 식에 넣어서 계산할 수 있기 때문.
표준 정규 분포
표준 정규분포는, 정규 분포를 평균이 0, 표준편차가 1이 되게 정규화한 분포이다.
정규화 수식: $ Z = \frac{X-\mu}{\sigma} $
일반 정규분포에서 표준 정규분포로 변환되는 것을 그래프로 나타내면,
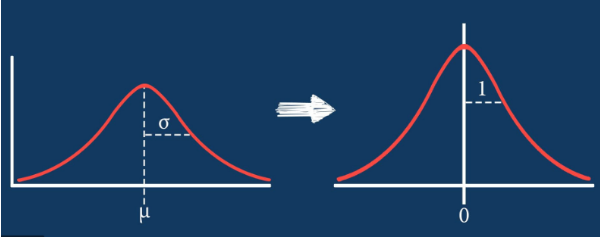
중심 극한 정리
중심 극한 정리는, "어떤 데이터에서 충분히 많은 표본을 뽑아내기만 하면, 그 표본 평균은 모평균을 중심으로 정규분포를 따른다"는 정리이다.
예를 들어, 어떤 모집단이 있는데 이 모집단의 평균은 36이고, 데이터의 꼬리가 오른쪽으로 긴 데이터라고 하자.
이 모집단에서 표본 샘플들을 여러 번 뽑아내면서 표본의 평균을 구해보면, 그 값들은 모평균인 36을 중심으로 한 정규분포를 띤다는 것이다.
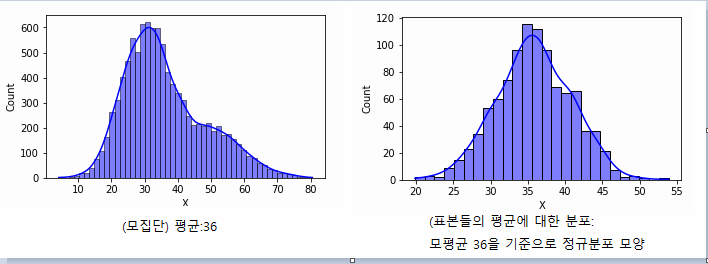
이처럼 어떠한 분포를 띤 집단에 대해서도, 표본을 뽑아내서 평균을 내면, 그 평균들은 정규분포를 띤다는 것은, 표본 평균들의 기댓값(=평균)이 모평균이 된다는 말과 같다. 즉, 표본들을 뽑아내 보면, 그 평균에 대한 평균은 모평균과 같다는 것이다. (매우 중요한 성질이다. 꼭 기억해 두자)
실제로 이상한 분포에 대해서도 표본 평균의 기댓값이 모평균과 같게 되는지 실험을 해보자.
# 쌍봉 데이터 만들기
import pandas as pd
import numpy as np
np.random.seed(123)
arr_pop = np.concatenate([
np.random.normal(loc=20, scale=10, size=5000),
np.random.normal(loc=80, scale=10, size=5000),
])
print('모평균', np.mean(arr_pop))
sns.histplot(arr_pop, kde=True, color='blue', bins=50)
plt.plot()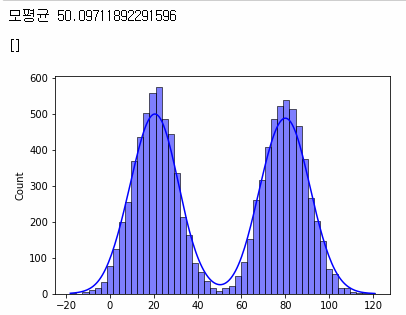
실행된 코드를 보면, 모평균은 50이고, 데이터의 모양은 쌍봉 형태로, 모평균인 50 주변 데이터는 없다.
이 만개의 데이터를 모집단으로 해서, 100개씩 무작위로 표본을 뽑아내서 평균을 구해보자.
lst = []
np.random.seed(123)
for i in range(5000):
idx = np.random.choice(10000, size=100)
lst.append(np.mean(arr_pop[idx]))
print('표본평균의 기댓값:', np.mean(lst))
fig = plt.figure(figsize=(5,3))
sns.histplot(lst, kde=True, color='blue')
plt.xlabel('X')
plt.plot()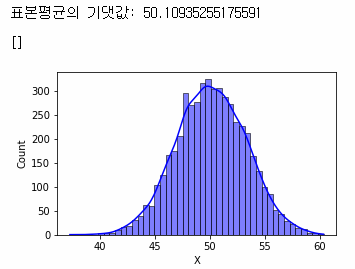
100개씩 뽑은 표본들에 대한 평균을 구하고, 그 평균들의 분포를 보면, 예상대로 모평균인 50을 중심으로 정규분포를 띰을 알 수 있다.
첨도(尖度, kurtosis, 커토시스)
첨도는, 분포가 중심에 어느 정도 몰려 있는가를 나타내는 값이다. 분포 곡선의 모양으로 얘기한다면, 곡선의 가운데 부분이 뾰쪽한 정도를 나타낸다고 할 수 있다.
정규분포의 첨도는 0이다. (기본적인 정의에 의하면 정규분포의 첨도는 3이지만, 일반적으로 정규분포의 첨도를 0으로 만들기 위해 3을 뺀 값을 정의해서 사용한다. Pandas의 kurtosis() 함수에 의해 계산되는 첨도 값도 정규분포의 첨도가 0이 되도록 조정된 값이 나온다. )
첨도의 값이 양수이면 곡선의 모양이 정규분포보다 더 뾰족하고, 음수이면 정규분포보다 더 퍼져있는 모양이 된다.
자료의 첨도 값을 k라 할 때,
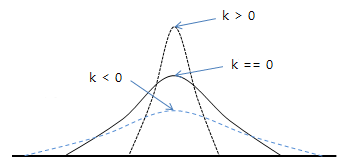
- k == 0 : 정규분포와 같음
- k > 0 : 정규분포보다 더 뾰족
- k < 0 : 정규분포보다 더 완만한 모양
Pandas에서 kurtosis 구하는 법: kurtosis 함수 이용
첨도 관련한 예를 보면,
# kurtosis K==0 k>0 k<0 인 데이터 만들기
import pandas as pd
import numpy as np
np.random.seed(0)
# 1)정규분포 k==0
arr_nor = np.random.normal(loc=50, scale=10, size=1000)
# 2) sharp k > 0
arr_sharp = np.concatenate([
np.random.normal(loc=50, scale=10, size=500),
np.random.normal(loc=50, scale=3, size=500),
])
# 3) smooth k < 0
arr_smooth = np.concatenate([
np.random.normal(loc=50, scale=10, size=400),
np.random.normal(loc=30, scale=10, size=300),
np.random.normal(loc=70, scale=10, size=300),
])
df = pd.DataFrame({
'normal':arr_nor,
'sharp':arr_sharp,
'smooth':arr_smooth
})
df.kurtosis()normal -0.040977
sharp 2.292955
smooth -0.682946
dtype: float64
import seaborn as sns
fig = plt.figure(figsize=(8,5))
sns.histplot(df['smooth'], kde=True, color='blue', label='smooth')
sns.histplot(df['normal'], kde=True, color='green', label='normal')
sns.histplot(df['sharp'], kde=True, color='red', label='sharp')
plt.xlabel('X')
plt.legend()
plt.show()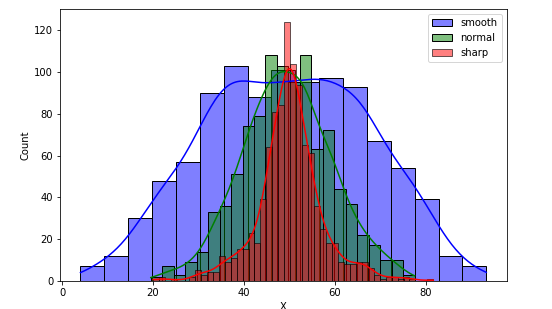
왜도(歪度, skewness, 스큐니스)
왜도는 비대칭도를 나타내는 값이다.
정규분포는 왜도 값이 0이고, 정규분포 대비 오른쪽으로 긴 꼬리를 가진 경우는(skewed to the right) 왜도 값이 양수이고, 왼쪽으로 긴 꼬리를 가진 경우는(skewed to the left) 왜도 값이 음수이다.
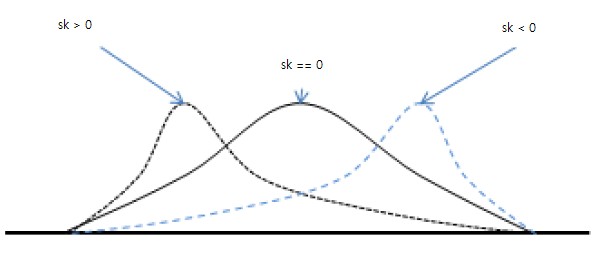
왜도의 경우 주의할 점은, "평균, 중앙값, 최빈값"의 위치이다.
정규분포(sk ==0)의 경우는 "평균 == 중앙값 == 최빈값"이다.
(sk > 0)의 경우는 "최빈값 < 중앙값 < 평균"
(sk < 0)의 경우는 "평균 < 중앙값 < 최빈값"
위 관계는 외우지 말고, 그래프를 통해서 이해하면 된다.
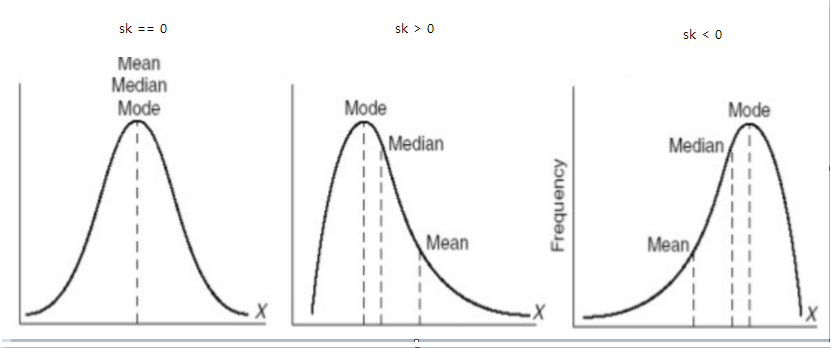
왜도 값에 따라서 어느 쪽으로 꼬리가 긴지 헷갈릴 수 있는데, 왜도 계산식이 $ (평균 - 중앙값) $에 비례한 값이라는 것을 기억하면 헷갈리지 않을 수 있다.
피어슨의 비대칭도(Perason's coefficient of skewness):
$ sk = \frac{3(\bar{x}-Md)}{s} $, s:표준편차
Pandas에서 왜도의 계산은 skew 함수를 사용하면 된다.
왜도가 다른 샘플 데이터를 만들어보고, skew함수에 의해 계산되는 값과 그래프를 그려보자.
import seaborn as sns
fig = plt.figure(figsize=(8,5))
sns.histplot(df['smooth'], kde=True, color='blue', label='smooth')
sns.histplot(df['normal'], kde=True, color='green', label='normal')
sns.histplot(df['sharp'], kde=True, color='red', label='sharp')
plt.xlabel('X')
plt.legend()
plt.show()normal 0.033910
right 0.752162
left -0.811409
dtype: float64
import seaborn as sns
fig = plt.figure(figsize=(8,5))
sns.histplot(df['right'], kde=True, color='blue', label='sk>0')
sns.histplot(df['normal'], kde=True, color='green', label='sk==0')
sns.histplot(df['left'], kde=True, color='red', label='sk<0')
plt.xlabel('X')
plt.legend()
plt.show()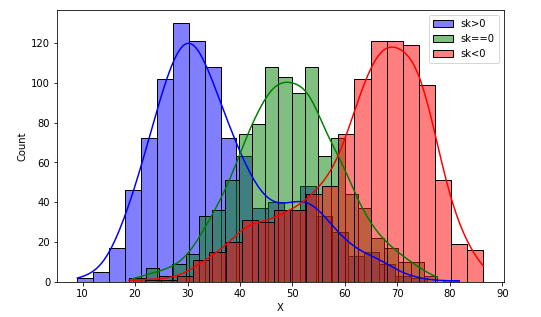
-끝-
다음 글: 2.1 분포 (예제 풀이)
'Information > 통계강의' 카테고리의 다른 글
| 2.2 가설 검정 (0) | 2021.02.17 |
|---|---|
| 2.1 분포 (예제 풀이) (0) | 2021.02.15 |
| 2. 분포 및 가설검정 (0) | 2021.02.14 |
| 1.3 데이터 스케일링 (예제 풀이) (0) | 2021.02.13 |
| 1.3 데이터 스케일링 (이론) (0) | 2021.02.13 |



