해밍 거리에 대해서 배울 때, d 비트의 에러 검출을 하려면 최소 해밍거리 $d_{min} = d + 1$이고(최소 해밍거리 $d_{min}$일때 에러 검출은 d-1개까지 가능하고), d 비트의 에러 보정이 가능하려면 최소 해밍거리 $d_{min}=2d+1$이 되어야 한다고 한다.
이 글에서는 왜 이렇게 되는지에 대해 설명한다.
해밍 거리 (Hamming Distance)
두 비트열 c1과 c2에 대한 해밍 거리는, 두 비트열의 같은 위치에 있는 서로 다른 비트의 개수이다.
헷갈리는 말이지만, 예를 들어보면 쉽게 이해될 것이다.
예를 들어 "111"과 "110"의 해밍거리는 1이다. 마지막 비트에 있는 값이 다르기 때문.
d(111,110) = 1
d(111,101) = 1
d(111,001)=2
d(111,000)=3
d(0001, 0000)=1
d(0001, 1110)=4
해밍 거리의 계산
해밍거리를 계산할 때, 눈으로 다른 비트의 수를 세도 되지만, 이를 계산식으로 표현한다면, 두 비트열에 대한 XOR를 하고, 그 값에서 1인 비트의 수를 세면 된다.
비트열에서 1인 비트의 수를 "해밍 무게(Hamming Weight)"라 하고, 기호로는 w를 사용한다.
w(00)=0
w(10)=1
w(110)=2
w(0001)=1
w(1101)=3이제 해밍거리의 계산을 XOR와 해밍 무게를 써서 표현하면 아래와 같이 된다.
$$ d(c1,c2) = w(c1 \wedge c2) $$
예를 들어 c1 = 1101, c2=1110 이라 하면,
c1과 c2의 비트별 xor 값은, c1 ^ c2 = 0011
xor한 값에 대한 해밍무게는,
w(c1 ^ c2) = w(0011) = 2
수식으로 표현했을 뿐, 두 비트열의 다른 비트열을 찾아내고(이 과정이 xor와 같다), 다른 비트열의 수를 세는 것과 동일한 과정이다.
해밍거리를 계산하는 이유 (에러 검출/보정 관점에서)
네트워크 통신에서 A가 B에게 비트 단위의 신호를 보내는 상황을 생각해 보자.
만약 1비트를 보내는 상황에서, A가 1비트를 보내고 B가 그 1비트를 받았을 때, 그 값은 0 아니면 1인데, 이 값이 전송 과정에서 뒤 바뀐 건지 알 수 있을까? B의 입장에서는 1비트 받은 정보만을 가지고는 그 값이 A가 진짜 보낸 것인지 뒤 바뀐 건지 알 수가 없다.
그렇다면, A가 정보를 보낼 때, 0을 보내는 경우는 "00"이라고 두 개의 비트를 보낸다고 하자. 1을 보낼 때는 "11"이라고 보내고. A와 B가 이렇게 약속하고, A가 "00"을 보냈을 때, B가 받을 수 있는 경우의 수를 생각해보자.
* A가 보낸 신호 00 혹은 11
* B가 받을 수 있는 신호: {00, 01, 10, 11}
* B가 신호 받은 후 유추한 값:
00 : 0으로 인식 --> Good or Fail
01 : ? (알수 없음. 그러나 전송에러가 발생했음을 알 수 있음)
10 : ? (알수 없음. 그러나 전송에러가 발생했음을 알 수 있음)
11 : 1로 인식 --> Good of Fail한 비트에 대한 전송에러가 발행한 경우는, 전송 에러가 발생했음을 알 수 있고, 두 비트 모두가 에러인 경우는 잘 못 인식하게 된다. (두 비트가 모두 같은 값인 00 혹은 11의 경우, 잘 전송되었는지 두 비트가 모두 에러인지 잘 모른다는 것이 정확한 표현이겠다.)
이제 연속된 세 개의 비트를 보내는 경우를 생각해보자. 0인 경우는 "000"을, 1인 경우는 "111"을 보내는 경우다.
* A가 보낸 신호: 000 (111로 보낸 경우도 유사한데, 일단, 000으로 보낸 케이스로 생각해보자)
* B가 받을 수 있는 신호 집합: {000, 001, 010, 011, 100, 101, 110, 111}
* B가 신호를 받고서 인식하는 값
000 : 0으로 인식
001 : 0으로 인식
010 : 0으로 인식
011: 1로 인식
100: 0으로 인식
101: 1로 인식
110 : 1로 인식
111 : 1로 인식
위 경우의 수를 정리하면,
1)에러 없는 경우
000: 에러 없고, 0이다. -> Good
2)1개 비트 에러의 경우
001, 010, 100 : 에러가 있고, 0인것 같다. -> Good
3)2개 비트 에러의 경우
011, 101, 110 : 에러가 있고, 1인것 같다. -> Fail
4)3개 비트 에러의 경우
111 : 에러 없고, 1이다. -> Fail3개 비트를 연속으로 보내는 방식에 대해서는, 1개 비트 에러가 발생한 것에 대해서는 보정이 되는데, 2개 이상의 비트가 에러가 생기는 것은 보정이 안된다. 근데, 2개 비트 에러의 경우 보정은 실패하지만 "전송 중 에러가 있다"라는 사실은 알 수 있다.
이제 위의 예를 가지고 일반화를 해보자.
첫 번째 2개의 연속된 비트인 "00" 혹은 "11"을 보내는 경우, 이 두 비트열에 대한 해밍거리는 2이다. 이 경우, 1개 비트 에러에 대해서는 "에러가 있었다"라는 검출은 가능했고, 2개의 비트 모두가 에러의 경우는 에러 자체가 있었는지 알 수 없었다.
두 번째 3개의 연속된 비트인 "000" 혹은 "111"을 보내는 경우, 이 두 비트열에 대한 해밍거리는 3이다. 이 경우, 1개 비트 에러에 대해서는 "에러 보정"까지 가능했고, 2개의 비트가 에러의 경우는 "에러 보정"은 안되고 "에러 검출"은 되었다. 3개의 비트 모두가 에러의 경우는 "에러 검출"도 안되었다.
정리하면,
해밍거리=2의 경우,
- 에러 검출: 1개 비트 에러의 경우
- 에러 보정: 불가
해밍거리=3의 경우,
- 에러 검출: 1~2개 비트 에러
- 에러 보정: 1개 비트 에러의 경우위 정리한 사항을 가지고 일반화를 해보면,
m 비트의 에러 검출을 위해서 필요한 최소해밍거리는,
$$ d_{min} = m + 1$$
m 비트의 에러 보정을 위해서 필요한 최소해밍거리는,
$$ d_{min} = 2m + 1$$
1개 비트 에러에 대한 보정이 가능하려면 최소해밍거리가 3이 되도록 코드를 보내야하고 ("000", "111" 처럼), 2개 비트에 대한 에러 보정이 가능하려면 최소 해밍거리가 5(=2x2 + 1)가 되도록 보내야 한다는 얘기다. (연속 코드로 얘기하면 "00000" "11111" 처럼 보내야 함)
해밍 코드 (Hamming Code)의 해밍 거리
해밍코드는 2의 지수승 자리(1,2,4,8,...)에 패리티 비트를 둬서, 전송된 전체 신호에 대한 자체 패리티 체크를 한 후 에러 보정을 하는 대표적인 FEC(Foward Error Correction) 방식이다.
(이 글에서는 해밍 코드에 대해서 구체적으로 들어가지는 않고, 해밍거리 관점에서 놓치기 쉬운 핵심 개념만을 얘기하겠다. 해밍코드가 어떻게 구성되고 구하는지는 다른 글에서 참조.)
4비트의 데이터를 해밍코드로 보내려면 3개의 패리티비트를 추가해서 모두 7비트를 보내게 된다. 그렇게 하면, 1개 비트에 대한 에러 보정이 가능하고, 2개 비트에 대한 에러 검출이 가능하다고 한다. 즉, 해밍코드의 최소해밍거리는 3이라는 것을 알 수 있다.
실제로 4개의 데이터 비트가 가질 수 있는 경우의 조합수는 16개이고(0000, 0001, 0010, ..., 1111), 이를 패리티 비트 3개를 부가해서 모두 나타내면 아래와 같다.
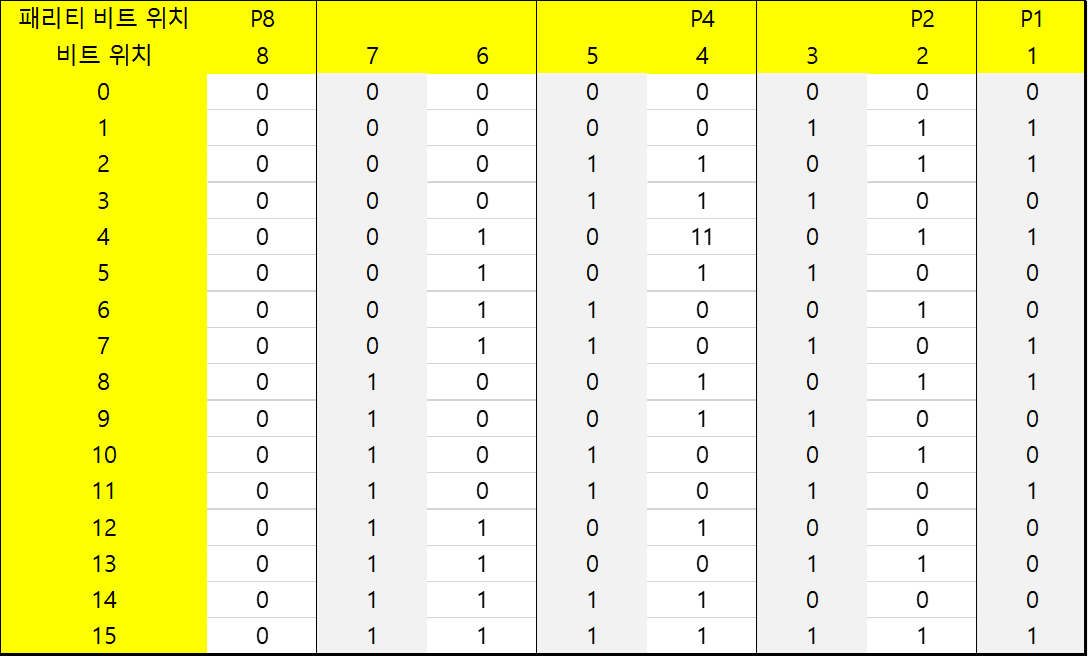
위와 같은 조합에서, 0과 1에 대한 해밍거리는 d(0,1)=3이고, d(1,2)=3, d(0,15)=7, ... 등 모든 조합을 해보면 최소한 해밍거리가 3이라는 것이다.
그래서, 해밍 코드를 사용했을 때 1개 비트 오류에 대해서만 보정이 가능한 것이고(2개 이상의 비트 에러에 대해서는 보정 못함), 2개 비트 에러에 대한 검출이 가능하다는 것이 된다.
해밍코드에서 1개 비트 에러 수정만 가능하다고 피상적으로 알고 있는 경우가 많은데, 위에서 얘기한 것처럼 해밍거리가 3이어서 그렇다는 것으로 생각해보면, 해밍코드에 대한 좀 더 깊은 생각을 할 수 있게 된다.
만약, 데이터 비트가 4개인 신호를 저 위쪽에서 얘기한 "연속코드"를 이용해서 보낸다면 어떻게 될까? 1개 비티에 대해서 보정이 가능하도록 하려면 연속 코드를 3개 보내야 한다고 했었다. 즉, 0인 비트는 "000" 1인 비트는 "111" 처럼.
그렇다면 4개의 비트가 "0101"이라면 "000 111 000 111"처럼 보내야 할 것이다. 따라서, 총 12비트가 필요.
그런데 해밍코드(Hamming Code)는 12비트가 아닌 7비트 만을 가지고 해밍거리가 3이 되도록 한 것이다. 이것이 해밍코드의 핵심이다. !! 2의 지수승 자리에 패리티 비트를 놓아서, 최소한의 패리티 비트 추가에 의해 해밍거리가 3이되도록 한 것임.
- 끝 -